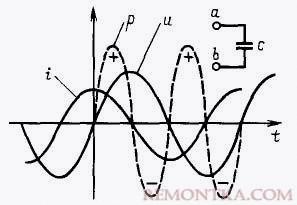
Что такое переменный ток

Если рассматривать постоянный ток, то он не всегда может быть идеально постоянным: напряжение на выходе источника может зависеть от нагрузки или от степени разряда аккумулятора или гальванической батареи. Даже при постоянном стабилизированном напряжении ток во внешней цепи зависит от нагрузки, что и подтверждает закон Ома. Получается, что это тоже не совсем постоянный ток, но переменным такой ток назвать тоже нельзя, поскольку направления он не меняет.

Переменным обычно называют напряжение или ток, направление и величина которого меняются не под действием внешних факторов, например нагрузки, а вполне «самостоятельно»: именно таким его вырабатывает генератор. К тому же, эти изменения должны быть периодическими, т.е. повторяющимися через определенный промежуток времени, называемый периодом.

Если же напряжение или ток меняется как попало, не заботясь о периодичности и иной закономерности, такой сигнал называется шумом. Классический пример — «снег» на экране телевизора при слабом эфирном сигнале. Примеры некоторых периодических электрических сигналов показаны на рисунке 1.

Для постоянного тока имеется всего две характеристики: это полярность и напряжение источника. В случае с переменным током этих двух величин явно недостаточно, поэтому появляются еще несколько параметров: амплитуда, частота, период, фаза, мгновенное и действующее значение .

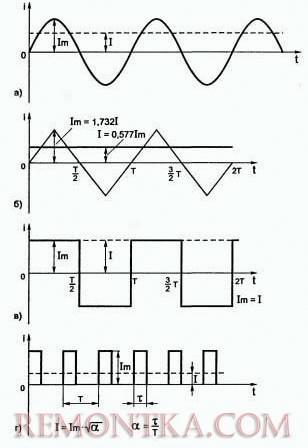
Рисунок 1. Примеры некоторых периодических электрических сигналов

Наиболее часто в технике приходится сталкиваться с колебаниями синусоидальной формы, причем, не только в электротехнике. Представьте себе автомобильное колесо. При равномерном движении по хорошей ровной дороге центр колеса описывает прямую, параллельную дорожному покрытию. В то же время, любая точка на периферии колеса перемещается по синусоиде относительно только что упомянутой прямой.

Сказанное может подтвердить рисунок 2, на котором показан графический метод построения синусоиды: кто хорошо учил черчение, тот прекрасно представляет, как выполняются подобные построения.

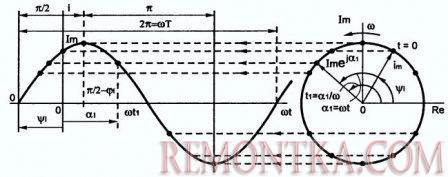
Рисунок 2. Графический метод построения синусоиды

Из школьного курса физики известно, что синусоида является наиболее распространенной и пригодной для изучения периодической кривой. В точности также синусоидальные колебания получаются в генераторах переменного тока , что обусловлено их механическим устройством.

На рисунке 3 показан график синусоидального тока.

Рисунок 3. График синусоидального тока

Нетрудно заметить, что величина тока изменяется по времени, поэтому ось ординат обозначена на рисунке как i(t), — функция тока от времени. Полный период тока обозначен сплошной линией и имеет период T. Если начать рассмотрение от начала координат, то видно, что сначала ток увеличивается, доходит до Imax, переходит через нуль, уменьшается до –Imax, после чего увеличивается и доходит до нуля. Далее начинается следующий период, что показано пунктирной линией.

В виде математической формулы поведение тока записывается так: i(t)= Imax*sin(ω*t±φ).

Здесь i(t) — мгновенное значение тока, зависящее от времени, Imax -амплитудное значение (максимальное отклонение от состояния равновесия), ω — круговая частота (2*π*f), φ — фазовый угол.

Круговая частота ω измеряется в радианах в секунду, фазовый угол φ – в радианах или градусах. Последний имеет смысл лишь в том случае, когда имеется два синусоидальных тока. Например, в цепях с конденсатором ток опережает напряжение на 90˚ или ровно на четверть периода, что и показано на рисунке 4. Если синусоидальный ток один, то можно двигать его по оси ординат как угодно, и от этого ничего не изменится.

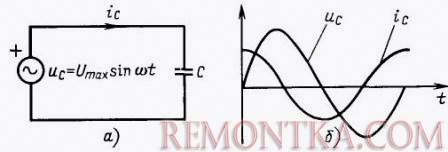
Рисунок 4. В цепях с конденсатором ток опережает напряжение на четверть периода

Физический смысл круговой частоты ω в том, какой угол в радианах «пробежит» синусоида за одну секунду.

Период – T время, за которое синусоида совершит одно полное колебание. То же относится и к колебаниям другой формы, например, прямоугольным или треугольным. Период измеряется в секундах или более мелких единицах: миллисекундах, микросекундах или наносекундах.

Еще один параметр любого периодического сигнала, в том числе и синусоиды это частота, сколько колебаний проделает сигнал за 1 секунду. Единицей измерения частоты является герц (Гц), названный по имени ученого XIX века Генриха Герца. Итак, частота 1Гц это есть ни что иное, как одно колебание/секунду. Например, частота осветительной сети 50Гц, то есть за секунду проходит ровно 50 периодов синусоиды.

Если известен период тока (можно измерить осциллографом ), то частоту сигнала поможет узнать формула: f=1/T. При этом, если время выражено в секундах, то результат получится в Герцах. И наоборот, T=1/f, частота в Гц, время получается в секундах. Например, при частоте 50 герц период получится 1/50=0,02сек, или 20 миллисекунд. В электричестве чаще применяются более высокие частоты: КГц – килогерцы, МГц – мегагерцы (тысячи и миллионы колебаний в секунду) и т.д.

Все сказанное для тока справедливо и для переменного напряжения: достаточно на рис 6 просто поменять букву I на U. Формула будет выглядеть вот так: u(t)=Umax*sin(ω*t±φ).

Этих разъяснений вполне достаточно для того, чтобы вернуться к опытам с конденсаторами и объяснить их физический смысл.

Конденсатор проводит переменный ток, что было показано в схеме на рисунке 3 (см. статью — Конденсаторы для электроустановок переменного тока ). Яркость свечения лампы увеличивается при подключении дополнительного конденсатора. При параллельном включении конденсаторов их емкости просто складываются, поэтому можно предположить, что емкостное сопротивление Xc зависит от емкости. Кроме того оно зависит еще от частоты тока, и поэтому формула выглядит так: Xc=1/2*π*f*C.

Из формулы следует, что с увеличением емкости конденсатора и частоты переменного напряжения реактивное сопротивление Xc уменьшается . Эти зависимости показаны на рисунке 5.

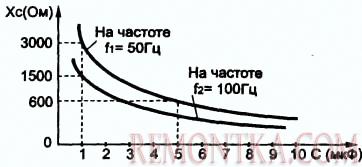
Рисунок 5. Зависимость реактивного сопротивления конденсатора от емкости

Если подставить в формулу частоту в Герцах, а емкость в Фарадах, то результат получится в Омах.

Будет ли греться конденсатор?

Теперь вспомним опыт с конденсатором и электросчетчиком, почему он не крутится? Дело в том, что счетчик считает активную энергию, когда потребителем является чисто активная нагрузка, например, лампы накаливания, электрочайник или электроплита. У таких потребителей напряжение и ток совпадают по фазе, имеют один знак: если перемножить два отрицательных числа (напряжение и ток во время отрицательного полупериода) результат по законам математики все равно положительный. Поэтому мощность таких потребителей всегда положительна, т.е. уходит в нагрузку и выделяется в виде тепла, как показано на рисунке 6 пунктирной линией.

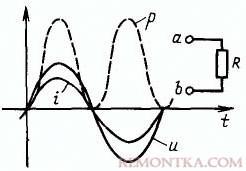
Рисунок 6.

В случае, когда в цепь переменного тока включен конденсатор ток и напряжение по фазе не совпадают: ток опережает по фазе напряжение на 90˚, что приводит к тому, что получается сочетание, когда ток и напряжение имеют разные знаки.

Рисунок 7.

В эти моменты мощность получается отрицательной. Другими словами, когда мощность положительная, конденсатор заряжается, а когда отрицательная — запасенная энергия отдается обратно в источник. Поэтому в среднем получается по нулям и считать тут просто нечего.

Конденсатор, если конечно он исправный, не будет даже нисколько нагреваться. Поэтому, часто конденсатор называют безваттным сопротивлением , что позволяет применять его в бестрансформаторных маломощных блоках питания. Хотя такие блоки не рекомендуется использовать ввиду их опасности, все-таки иногда это делать приходится.

Перед тем, как устанавливать в такой блок гасящий конденсатор , его следует проверить простым включением в сеть: если за полчаса конденсатор не нагрелся, то его смело можно включать в схему. В противном случае его придется просто без сожаления выбросить.

Что показывает вольтметр?

При изготовлении и ремонте различных устройств, хоть и не очень часто, но приходится мерить переменные напряжения и даже токи. Если синусоида ведет себя так неспокойно, то вверх, то вниз, что будет показывать обычный вольтметр?

Среднее значение периодического сигнала, в данном случае синусоиды, подсчитывается как площадь, ограниченная осью абсцисс и графическим изображением сигнала, деленная на 2*π радиан или период синусоиды. Поскольку верхняя и нижняя часть абсолютно одинаковы, но имеют разные знаки, среднее значение синусоиды равно нулю, и мерить его совсем не нужно, и даже просто бессмысленно.

Поэтому измерительный прибор показывает нам среднеквадратичное значение напряжения или тока. Среднеквадратичным называется такое значение периодического тока, при котором на одной и той же нагрузке выделяется то же количество теплоты, что и на постоянном токе. Иными словами лампочка светит с той же яркостью.

Формулами это описывается вот так: Iсрк=0,707*Imax= Imax/√2 для напряжения формула та же, достаточно поменять одну букву Uсрк=0,707*Umax=Umax/√2. Именно эти значения показывает измерительный прибор. Их можно подставлять в формулы при расчете по закону Ома или при расчете мощности.

Но это далеко не всё, на что способен конденсатор в сети переменного тока. В следующей статье будет рассмотрено использование конденсаторов в импульсных схемах, фильтрах верхних и нижних частот, в генераторах синусоиды и прямоугольных импульсов.

Продолжение статьи: Конденсаторы в электронных схемах