Среднее значение переменного синусоидального напряжения или тока

Говоря о величине, изменяющейся по синусоидальному (гармоническому) закону, можно за половину периода определить ее среднее значение. Поскольку ток в сети у нас в подавляющем большинстве случаев синусоидальный, то для этого тока также легко может быть найдена средняя его величина (за половину периода), достаточно прибегнуть к операции интегрирования, установив пределы от 0 до Т/2. В результате получим:

Подставив Пи = 3,14, найдем среднюю, за половину периода, величину синусоидального тока в зависимости от его амплитуды. Аналогичным образом находится среднее значение синусоидальной ЭДС или синусоидального напряжения U:

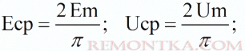
Действующее значение тока I или напряжения U

Однако среднее значение не так широко применяется на практике, как действующее значение синусоидального тока или напряжения. Действующее значение синусоидально меняющейся во времени величины — есть среднеквадратичное, другими словами — эффективное ее значение.

Эффективное (или действующее) значение тока или напряжения находится так же, путем интегрирования, но уже по отношению к квадратам, и с последующим извлечением квадратного корня, причем пределы интегрирования теперь — целый период синусоидальной функции.

Итак, для тока будем иметь:

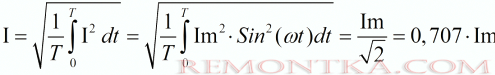
Подставив значение корня из 2, получим формулу для нахождения эффективного (действующего, среднеквадратичного) значения тока, напряжения, ЭДС — по отношению к амплитудному значению. Эту формулу можно встретить очень часто, ее используют всюду в расчетах, связанных с цепями переменного синусоидального тока:

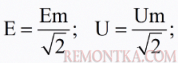
С практической точки зрения, если сравнить тепловое действие тока переменного синусоидального с тепловым действием тока постоянного непрерывного, на протяжении одного и того же периода времени, на одной и той же активной нагрузке, то выяснится, что выделенная за период синусоидального переменного тока теплота окажется равна выделенной за это же время теплоте от тока постоянного, при условии, что величина постоянного тока будет меньше амплитуды тока переменного в корень из 2 раз:

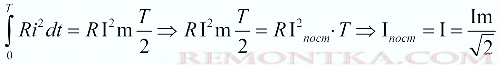
Это значит, что действующее (эффективное, среднеквадратичное) значение синусоидального переменного тока численно равно такому значению постоянного тока, при котором тепловое действие (выделяемое количество теплоты) этого постоянного тока на активном сопротивлении за один период синусоиды равно тепловому действию данного синусоидального тока за тот же период.

Аналогичным образом находится действующее (эффективное, среднеквадратичное) значение синусоидального напряжения или синусоидальной ЭДС.

Подавляющее большинство современных портативных измерительных приборов , измеряя переменный ток или переменное напряжение, показывают именно действующее значение измеряемой величины, то есть среднеквадратичную величину, а не ее амплитуду и не среднее значение за полпериода.

Если других уточняющих настроек на приборе нет, а стоит значок ~I или ~U – измерены будут действующие значения тока и напряжения. Обозначения для конкретно амплитуды или конкретно действующего — Im (m — maximum – максимум, амплитуда) или Irms (rms — Root Mean Square – среднеквадратичное значение).