После описания нескольких квантовых алгоритмов, мы можем перейти к рассмотрению ещё одного алгоритма, который наделал больше всего шума, и, собственно, из-за которого, по мнению многих, новая вычислительная модель, основанная на законах квантовой механики, получила такое развитие. Это алгоритм Шора для факторизации целых чисел, являющихся произведением двух простых нечётных чисел.

Примечание: Эта статья является продолжением в цикле статей по модели квантовых вычислений, поэтому если начать читать её без ознакомления с предыдущими статьями цикла, что-то может показаться непонятным. Так что читателя, который впервые набрёл на эти мои заметки, я отправляю к первым статьям:

• Слово малое об обратимых вычислениях ;
• Реализация алгоритма Дойча на языке Haskell ;
• Квантовая схемотехника: некоторые приёмы и техники ;
• Разворачиваем язык квантового программирования Quipper ;
• Продолжаем изучать квантовые вычисления: алгоритм Дойча-Йожи ;
• Квантовый поиск при помощи алгоритма Гровера ;
• Реализация алгоритма Саймона на языке Haskell ;

Всё дело в том, что именно на гипотезе алгоритмической сложности задачи факторизации числа основаны многочисленные современные алгоритмы и системы криптографии. Найденный Питером Шором в 1994 году алгоритм позволяет решить эту задачу за полиномиальное время (стало быть, полиномиально количество гейтов) и на полиномиальном количестве кубитов, в то время как классические алгоритмы решают её за суперполиномиальное (субэкспоненциальное) время. А это значит, что как только квантовый компьютер с достаточным количеством кубитов будет создан, вся современная криптография окажется под угрозой компрометации. Собственно, она и будет скомпрометирована тут же, поскольку любая информация, сокрытая с использованием этого подхода, может быть получена любым лицом, у кого имеется доступ к такому квантовому компьютеру.

Поскольку алгоритм Шора разительно отличается от всех ранее рассмотренных алгоритмов в части наличия серьёзной прикладной значимости, сам алгоритм более сложен с точки зрения математики и архитектуры. Здесь уже задействованы две вычислительные парадигмы — классическая часть готовит входные данные для алгоритма Шора, а также управляет циклами и возвратами в целях нахождения правильного результата; ну а квантовая часть, как это обычно бывает, просто исполняет линейную последовательность унитарных преобразований над специально подготовленными состояниями входных кубитов.

Немного математики

Итак, алгоритм факторизации Шора… Его суть заключается в сведении задачи факторизации к задаче поиска периода функции. Если известен период функции, то факторизация осуществляется при помощи алгоритма Евклида за полиномиальное время на классическом компьютере. И вот квантовая часть алгоритма факторизации как раз занимается поиском периода функции. А классическая часть алгоритма сначала специальным образом готовит оную функцию, а потом проверяет найденный квантовой частью период на достаточность для решения задачи. Если период найден правильно (алгоритм вероятностный, так что может найти не то, что хочется), то задача решена. Если же нет, то квантовая часть алгоритма прогоняется ещё раз. А, поскольку, проверка правильности решения для задачи факторизации очень проста (умножили два числа да сравнили с третьим), то эту часть алгоритма вообще можно не принимать во внимание с точки зрения подсчёта сложности.

Чтобы не быть голословными и слишком теоретизированными, давайте попробуем рассмотреть алгоритм факторизации Шора на простом примере. Для этого просто разложим на простые множители некоторое число, являющееся произведением двух и в точности двух простых чисел, ни одно из которых не является числом 2. Поскольку исследователи из Международных Деловых Машин уже факторизовали на своём прототипе квантового компьютера число 15, здесь предлагается факторизовать число 21, хотя это вообще не принципиально, поскольку главное в рассмотрении то, чтобы хватило вычислительных мощностей.

Сначала рассмотрим алгоритм вручную, а потом, как это полагается, напишем программу на языке Haskell с использованием всё того же ранее разработанного набора функций, при необходимости дополняя его.

Для того чтобы факторизовать число при помощи алгоритма Шора, необходимо найти период периодической функции f(x) = a x (mod M) , где a — некоторый параметр, выбираемый произвольно до старта алгоритма, а M — число, которое необходимо факторизовать. Самое главное ограничение заключается в том, чтобы у чисел a и M не было общих делителей, больших 1. Поскольку мы хотим факторизовать число 21, в качестве параметра a возьмём число 2. Обычно это значение и берут (чаще всего оно подходит), но иногда необходимо брать другое значение, и критерии выбора будут описаны позже.

Теперь составим такую таблицу:

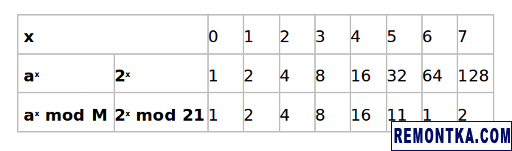
Из этой таблицы видно, что в данном конкретном примере периодом функции является значение r = 6. Другими словами, чтобы найти период при помощи такой таблицы, необходимо найти минимальное значение x, большее 1, для которого a x ? 1 (mod M) . Соответственно, алгоритм Шора выигрывает именно на этом этапе, поскольку при помощи модели квантовых вычислений найти период функции можно с полиномиальной сложностью, чего нельзя сделать в рамках классической вычислительной модели.

Далее остаётся дело техники. Множители числа M определяются как наибольшие общие делители (НОД) между a (r/2) ± 1 и M. Отсюда следует ещё одно ограничение на значение параметра a, выбираемого перед запуском алгоритма, — найденный период должен быть чётным, то есть нацело делиться на 2. Поскольку в рассматриваемом примере r = 6, данное условие выполнено. Так что в качестве a (r/2) ± 1 получаются два числа — 2 3 − 1 = 7 и 2 3 + 1 = 9 . Вычислить наибольшие общие делители можно с помощью уже упоминавшегося алгоритма Евклида, и для чисел 7 и 9 с числом 21 это будет пара (7, 3). Собственно, эта пара и есть разложение числа 21 на простые множители.

Теперь рассмотрим структурированное и более или менее формализованное описание алгоритма факторизации. Сам алгоритм состоит из следующих шагов:

1. Выбрать случайное число a, меньшее M: a < M.
2. Вычислить НОД(a, M). Это может быть сделано при помощи алгоритма Евклида.
3. Если НОД(a, M) не равен 1, то существует нетривиальный делитель числа M, так что алгоритм завершается (вырожденный случай).
4. В противном случае необходимо использовать квантовую подпрограмму поиска периода функции f(x) = a x mod M .
5. Если найденный период r является нечётным, то вернуться на шаг 1 и выбрать другое число a.
6. Если a (r/2) ? M − 1 (mod M), то вернуться на шаг 1 и выбрать другое число a.
7. Наконец, определить два значения НОД(a (r/2) ± 1, M) , которые и являются нетривиальными делителями числа M.

Собственно, здесь все шаги, кроме 4-го, представляют собой тривиальные действия, которые мы рассматривать не будем. Имеет смысл рассмотреть только четвёртый шаг, на котором выполняется квантовый алгоритм в виде подпрограммы полного алгоритма факторизации Шора.

Здесь важным моментом является выбор количества кубитов, которые будут использованы в квантовой схеме. В соответствии с рекомендациями автора алгоритма необходимо выбрать такое количество кубитов q, при котором выполняется неравенство M 2 ? 2q < 2M 2 . Выполнение этого неравенства обозначает, что данного количества кубитов будет достаточно для того, чтобы выполнить функцию, для которой ищется период, достаточное количество раз, чтобы сработала конструктивная интерференция. В рассматриваемом примере, когда M = 21, достаточным числом q будет, очевидно, число 9:

Итого, требуется 9 кубитов во входном квантовом регистре и столько же кубитов во вспомогательном квантовом регистре, который используется для получения значения квантового оракула, в который необходимо преобразовать функцию. Стало быть, всего необходимо 18 кубитов, а это значит, что для факторизации выбранного числа требуется матрица размера 2 18 ? 2 18 , то есть 262144 ? 262144. Такой размер гейта не очень способствует его построению в ручном режиме, поэтому здесь мы воспользуемся некоторым упрощением, которое скажется только на уровне точности получаемых результатов (но не на принципе). Мы будем использовать всего 9 кубитов, причём 4 из них будут рабочими, а 5 — вспомогательными. Выбранное число вспомогательных кубитов вполне достаточно для представления всех значений рассматриваемой периодической функции, поскольку максимальным её значением является 16, для представления которого требуется как раз 5 битов.

Построение оракула

Для построения оракула на этом количестве кубитов можно воспользоваться электронными таблицами. Для этого надо просто составить такую же таблицу, которая составлялась при построении оракулов во всех предыдущих примерах, только теперь в ней будет уже 512 строк. Эти строки можно заполнить в автоматизированном режиме при помощи инструментов, предлагаемым оболочкой для обработки электронных таблиц. Но всё равно это будет очень долго и муторно.

Тем не менее, посмотрим, как эта таблица будет выглядеть для выбранного количества кубитов — у нас используется 4 входных и 5 вспомогательных кубитов. То, как будет выглядеть заголовок такой таблицы, а также начальные и конечные строки, показано в следующей таблице.

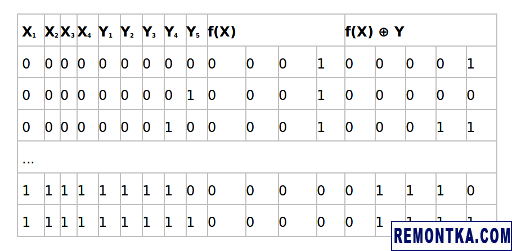
Как видно, здесь нет ничего необычного. Оракул строится стандартным образом, то есть абсолютно так же, как и для всех прочих алгоритмов (если только для какого-то алгоритма не указана иная техника построения оракула).

Теперь эту таблицу необходимо преобразовать в матрицу. Для этого можно воспользоваться упрощённым методом, применив для него небольшого рода автоматизацию. Поскольку каждая строка в этой таблице соответствует строке в матрице оракула (точь в точь вместе с номерами строк), то необходимо лишь узнать, каким столбцам матрицы оракула соответствуют строки. Для этого надо просто взять и для каждой строки посчитать десятичное число, получаемое из двоичного, которое, в свою очередь, составляется из первых четырёх и последних пяти столбцов указанной таблицы. Сделать это можно всё теми же средствами электронной таблицы. В итоге получится список из 512 целых чисел, в котором позиция числа определяет номер строки в матрице оракула, а само число определяет номер столбца в этой же матрице. Остаётся написать функцию для преобразования такого списка в саму матрицу. Это не слишком сложно:

Здесь список oracleList представляет собой тот самый список из 512 элементов. Мы не будем приводить его здесь, разве что только его начало:

Функция qubitFromInt строит векторное представление кубита, заданного десятичным числом. Она использует ранее определённую функцию changeElement, которая меняет элемент в заданном списке на заданной позиции. Поскольку последняя функция нумерует элементы в списке, начиная с 1, а здесь имеет место нумерация с 0, то приходится к номеру числа в списке прибавлять единицу. И в итоге эта функция выдаёт список из 511 нулей и 1 единицы, которая стоит на заданном месте.

Но иногда нам надо будет строить оракулы и для большего количества кубитов, так что таким подходом не обойтись. Придётся автоматизировать дальше и написать функцию для вычисления списка, который используется при построении оракула. Это сделать очень несложно:

Если эту функцию запустить со следующими параметрами:

… то в результате получится абсолютно такой же список, как и oracleList. И эта функция будет использоваться далее для построения полноценного оракула на 9 кубитах. Это делается при помощи переопределения функции oracle:

Надо отметить, что функция makeOracleList позволяет строить оракулы для произвольных функций типа (Int -> Int), так что её резонно разместить в модуле, где приводятся примитивы для описания гейтов.

Квантовое преобразование Фурье

Теперь можно реализовать «сердце» этого алгоритма, а именно квантовое преобразование Фурье. Как ни странно, его проще всего реализовать на основе аналитической формулы, при помощи которой вычисляются элементы матрицы, представляющей гейт. Вот эта формула:

Здесь m и n — номера позиции элемента по строкам и столбцам, при этом счёт начинается с 1. При помощи формулы Эйлера (e ix = cos x + i sin x) гейт для квантового преобразования Фурье кодируется следующим образом:

Городить что-то на основе квантовых схем в данном случае было бы просто неразумно. А так получается простейшая функция, которая ещё и строит гейт для заданного количества кубитов (параметр q).

Реализация алгоритма

Теперь перед реализацией квантовой процедуры поиска периода надо определить несколько вспомогательных функций и констант (и далее по тексту такие константы будут определены ещё в большем количестве):

Константа numberToFactor задаёт число, которое мы будем разлагать на простые множители. Константа simpleNumberпредставляет собой взаимно простое число с предыдущей константой. Далее константы nofAncillas, nofWorkingQubits и nofQubits представляют количество вспомогательных и рабочих кубитов, а также общее количество кубитов в квантовой схеме. Такой подход к параметризации алгоритма выбран для того, чтобы не определять функции с большим количеством аргументов, но при этом оставалась бы возможность быстро менять параметры алгоритма в одном месте.

Функция periodicFunction являет собой как раз ту периодическую функцию, задачу поиска периода которой и выполняет квантовая подпрограмма алгоритма Шора. Как видно, здесь во всю используются определённые ранее константы.

Теперь можно реализовать и квантовую схему в виде функции. Она будет выглядеть вот так:

Это определение соответствует следующей диаграмме квантовой схемы:

Надеюсь, что к этому времени читатель уже настолько поднаторел в понимании модели квантовых вычислений, что может сначала прочитать код функции, а затем восстановить по нему диаграмму квантовой схемы. Это очень полезный навык, так что всем читающим эти строки рекомендуется в нём потренироваться.

Проблемой (или, скорее, особенностью) алгоритма Шора является то, что результат измерения, полученный после выполнения quantumFactoring представляет собой некоторое грубое приближение к отношению некоторого числа к периоду функции. Получить из этого значение самого периода можно только посредством запуска приведённой квантовой схемы некоторое количество раз, сбора результатов с дальнейшей манипуляцией ими специальным образом. К настоящему времени разработано несколько различных методов вычисления периода функции на основании списка собранных результатов, причём разные методы обладают разной сложностью и требуют различное количество кубитов для своей работы. Самым простым (но чуть более трудоёмким) способом получения периода является метод цепных дробей.

Цепной дробью называется представление вещественного числа в виде:

… где a ₀ — целое, а остальные коэффициенты натуральные. Рациональные числа могут быть представлены конечной цепной дробью, а иррациональные — бесконечной.

При помощи цепных дробей можно найти хорошие приближения к искомому периоду периодической функции, при этом размер этого приближения ограничен некоторым количеством битов (равным количеству рабочих кубитов). Для выполнения этих громоздких вычислений имеет смысл написать специальные функции и другие определения. Начнём с типа для представления цепных дробей:

Цепная дробь — это просто список её коэффициентов. Мы заворачиваем список в новый конструктор изоморфного типа newtype в целях инкапсуляции поведения.

Теперь определим функции преобразования рационального числа в цепную дробь и обратно. Это довольно просто в полном соответствии с математическими правилами (разработанными ещё самим Эйлером):

В дополнение к этим функциям необходимо определить ещё и функцию для преобразования числа из цепной дроби в обычную так, что числитель и знаменатель ограничены определённым количеством бит. Эта функция как раз и потребуется для приближённого вычисления периода. Вот её определение:

Имея такие функции, несложно написать определение для получения периода на основании измеренного значения входного реестра кубитов. Вот оно:

Поскольку эта функция довольно важна с точки зрения алгоритма факторизации, её необходимо рассмотреть подробнее. На вход ей подаётся число s, полученное после измерения входного реестра. Далее строится дробь, в числителе которой стоит это число, а в знаменателе — 2 в степени равной количеству входных кубитов. Эта дробь далее преобразуется в цепную, а затем обратно в обычную, но с ограничением по количеству бит для её представления. После этого берётся знаменатель, который и возвращается в качестве результата. В этом и состоит суть метода цепных дробей в применении к алгоритму факторизации Шора.

Эксперимент

В общем-то, всё готово для реализации полного цикла алгоритма. Но остаётся не совсем ясным вопрос о том, сколько раз запускать квантовую подпрограмму, а сколько раз сам алгоритм факторизации, чтобы вероятность получения правильного ответа была большая, но при этом тратилось бы не так уж много временных ресурсов. Для получения ответов на эти вопросы можно провести небольшой, но занимательный эксперимент.

Для эксперимента напишем несколько функций. Первая функция возвращает частотную вероятность получения правильного ответа в зависимости от количества запусков квантовой подпрограммы и самого квантового алгоритма. Вот её определение:

Эта функция 100 раз запускает полный цикл квантового поиска простых делителей, в котором сам алгоритм запускается n раз, а квантовая подпрограмма в рамках каждого запуска алгоритма запускается m раз. За это количество запусков считается количество успешного разложения числа — берётся просто сумма элементов списка, в котором значение 1 обозначает, что простые делители найдены, и 0 — то, что не найдены. Так что результатом является примерное процентное соотношение корректной отработки алгоритма.

Здесь есть вызов функции collectPeriods, которая собирает большинство возможных периодов периодической функции для числа, которое факторизацией при помощи алгоритма Шора. Вот её определение:

Опять же эта функция n раз запускает следующий процесс (получается, что сам алгоритм факторизации): производится вызов квантовой подпрограммы m раз, результаты её работы собираются в список, который сортируется и группируется, дубликаты удаляются, а над полученным списком производится фильтрации в соответствии с критериями получения хорошего периода, описанными в математическом определении алгоритма Шора. Сначала удаляются нечётные периоды, а затем такие, которые дают тривиальные делители (для них
a (r/2) = M − 1 (mod M) ). Результирующий список подходящих периодов и возвращается.

Как видно, здесь использована функция findRandomPeriod, которая запускает квантовую подпрограмму заданное количество раз. Рассмотрим её определение:

Данное определение довольно громоздко, поэтому требуются пояснения. Функция запускает m раз квантовую подпрограмму, которую мы уже определили (quantumFactoring). Далее собранные результаты работы этой подпрограммы собираются в список, который подвергается следующим манипуляциям. Сначала вычленяются результаты измерения только входных кубитов, поскольку вспомогательные нас не интересуют. Далее этот список сортируется, группируется, из него удаляются дубликаты. Заодно при удалении дубликатов считается количество удалённых дубликатов (то есть, получается, что это опять частотная вероятность проявления такого результата в рамках всех измерений), а само значение переводится из строки в число. Далее список фильтруется так, что из него удаляются все результаты, частотная вероятность проявления которых меньше, чем десятикратно уменьшенное число запусков. Такие отфильтрованные результаты являются помехами и в алгоритме не рассматриваются. Далее отфильтровываются нулевые результаты, поскольку нулевой результат тривиален и ведёт к получению тривиальных делителей. После этого при помощи вызова функции getPeriod получаются все возможные периоды по результатам выполнения квантовой подпрограммы. И затем (и это очень важно) вычисляется наименьшее общее кратное всех таких периодов, которое и возвращается в качестве результата.

Вуаля! Этот набор функций позволяет провести исследование и узнать частотную вероятность получения корректного результата. Но для массового запуска функции investigate желательно немного подготовиться. Для этого напишем ещё одно определение:

Эта функция просто запускает двойной цикла запуска функции investigate в заданных интервалах сбора информации, а результаты выводит на экран в удобочитаемом виде. Данная функция была запущена на интервалах [1..10] для количества вызова алгоритма и [1..50] для количества вызова квантовой подпрограммы. В результате был построен вот такой примечательный график:

Этот график представляет довольно красивый с эстетической точки зрения результат. И при помощи него же можно вполне определить, что для корректного получения результата с вероятностью, приближающейся к 90 %, достаточно запустить алгоритм 10 раз, в каждом запуске использовать квантовую подпрограмму 3 раза. Поэтому так и определим:

Окончательная реализация алгоритма

Теперь можно написать определение функции main, которая будет факторизовать число numberToFactor. Сделаем её дружелюбной к пользователю:

В результате выполнения этой функции на экран консоли будет выведено что-то типа:

Собственно, это всё. Но для закрепления материала можно реализовать тот же самый алгоритм, но без квантовой части. Поиск периода будет осуществляться простым перебором списка. Вот определение функции:

Заключение

При подготовке этой статьи был создан файл с электронной таблицей, в которой рассматривается алгоритм факторизации, а также приводятся результаты экспериментирования, описанные выше. Кому интересно, может запросить у меня этот файл здесь в комментариях или в личном сообщении — вышлю на почту. Ну а заинтересованному читателю рекомендуется изменить значение константы numberToFactor на 15 (это ещё одно число, которое можно разложить на простые множители при помощи алгоритма Шора на имеющихся количествах кубитов) и посмотреть, что получится.

Код, описанный в этой небольшой заметке, можно получить здесь .

Дополнение: Факторизация числа при помощи квантового алгоритма Гровера