SciPy — это библиотека для языка Python , содержащая различные методы для инженерных и научных расчетов. При помощи SciPy можно считать интегралы, решать задачи оптимизации, обрабатывать изображения, и не только. Особый интерес представляют методы для расчета DSP-фильтров . Давайте разберемся, как ими пользоваться.
Нам понадобятся следующие зависимости:
Чтобы не возникло конфликтов с другими проектами, не лишено смысла завести отдельную песочницу при помощи virtualenv . SciPy тесно связан с Matplotlib и NumPy . Эти библиотеки мы уже проходили. Не будем на них задерживаться.
Воспользуемся следующим шаблоном скрипта:
# firdesign.py
# Aleksander Alekseev, 2023
# https://remontka.com/scipy-dsp-filter-design/
import numpy as np
import scipy . signal as signal
import matplotlib . pyplot as plt
sample_rate = 44100.0 # Sample rate, Hz
nyq_rate = sample_rate / 2.0 # Nyquist rate
# ========================================
# Create a low-pass FIR filter
numtaps = 61
cutoff_hz = sample_rate/ 4
taps = signal . firwin ( numtaps , cutoff_hz/nyq_rate , window = ‘hamming’ )
# ========================================
for t in taps:
print ( «{},» . format ( t ) )
# Plot the filter coefficients
plt. figure ( 1 )
plt. plot ( taps , ‘o-‘ , linewidth = 2 )
plt. title ( ‘Impulse response’ )
plt. grid ( True )
# Plot the magnitude response
w , h = signal . freqz ( taps )
plt. figure ( 2 )
plt. plot ( ( w/np. pi ) *nyq_rate , 20 *np. log10 ( np. abs ( h ) + ( 1.0e-10 ) ) ,
linewidth = 2 )
plt. xlabel ( ‘Frequency (Hz)’ )
plt. ylabel ( ‘Gain (dB)’ )
plt. ylim ( — 95 , 5 )
plt. title ( ‘Magnitude Response’ )
plt. grid ( True )
# Plot the phase response
# see https://dsp.stackexchange.com/a/50564/36360
plt. figure ( 3 )
h = h*np. exp ( 1j*w* ( numtaps// 2 ) )
plt. plot ( ( w/np. pi ) *nyq_rate , 180 *np. angle ( h ) /np. pi , linewidth = 2 )
plt. xlabel ( ‘Frequency (Hz)’ )
plt. ylabel ( ‘Phase (deg)’ )
plt. title ( ‘Phase Response’ )
plt. grid ( True )
plt. show ( )
Выделенный фрагмент будем заменять, чтобы получались различные фильтры.
В приведенном примере рассчитывается FIR фильтр, представляющий собой ФНЧ. Количество коэффициентов определено по знакомой нам эвристике :
numtaps = 60/(22*(11_000/44100-9_000/44100)) = 60.14
Вот АЧХ фильтра:
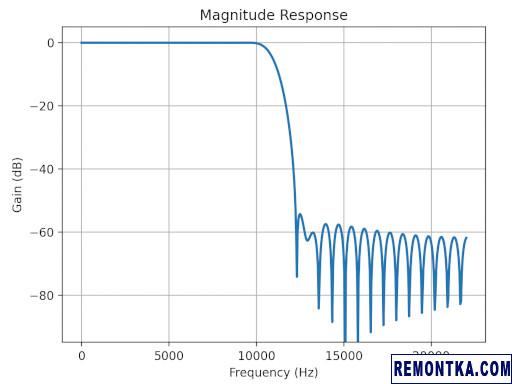
… а вот импульсная характеристика, она же коэффициенты фильтра:
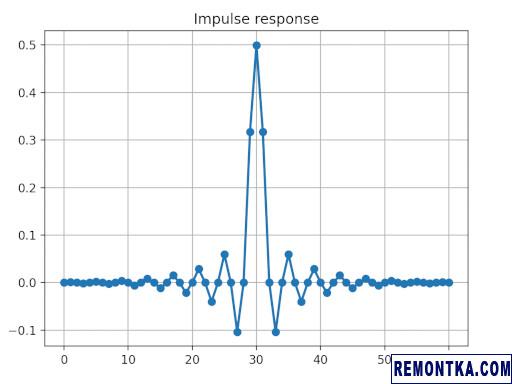
Примерно половина коэффициентов равна нулю. Это потому что фильтр имеет частоту среза sample_rate/4 . Еще можно заметить, что коэффициенты фильтра симметричны. Благодаря этому факту можно сократить количество умножений еще в два раза.
Альтернативный код:
# relative to the Nyquist rate
width = 2000 /nyq_rate
# The desired attenuation in the stop band, in dB
ripple_db = 60.0
# Compute the order and Kaiser parameter for the FIR filter
numtaps , beta = signal . kaiserord ( ripple_db , width )
# The cutoff frequency of the filter.
cutoff_hz = 10000
# Use firwin with a Kaiser window to create a lowpass FIR filter
taps = signal . firwin ( numtaps , cutoff_hz/nyq_rate ,
window = ( ‘kaiser’ , beta ) )
Здесь мы получаем фильтр, имеющий 81 коэффициент. Его АЧХ лучше, однако вычислительная сложность существенно выше.
Еще при помощи метода firwin() можно рассчитать ФВЧ:
cutoff_hz = 10000
taps = signal . firwin ( numtaps , cutoff_hz/nyq_rate ,
window = ‘hamming’ , pass_zero = False )
… полосовой фильтр:
taps = signal . firwin ( numtaps , [ 5000 /nyq_rate , 15000 /nyq_rate ] ,
window = ‘hamming’ , pass_zero = False )
… и режекторный фильтр:
taps = signal . firwin ( numtaps , [ 5000 /nyq_rate , 15000 /nyq_rate ] ,
window = ‘hamming’ )
Метод remez() также предназначен для расчета FIR фильтров. Но в отличие от firwin() , он может генерировать дифференциаторы, а также преобразователи Гильберта. И те и другие играют важную роль в SDR.
Преобразователь Гильберта — это фазовый фильтр, или all-pass filter , вносящий во входные сигналы фазовый сдвиг 90°. Рассчитаем его при помощи remez() :
window = signal . windows . kaiser ( numtaps , beta = 8 )
taps = signal . remez ( numtaps , [ 0 , nyq_rate ] , [ 1 ] ,
type = ‘hilbert’ , fs = sample_rate )
taps = taps * window
АЧХ фильтра:
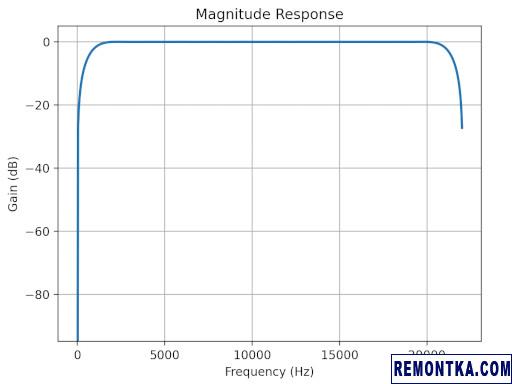
… ФЧХ фильтра:

… и его коэффициенты:

Заметьте, что половина коэффициентов снова оказалась равна нулю. Это общее свойство преобразователей Гильберта с нечетным количеством коэффициентов. Тот факт, что фильтр подавляет постоянные сигналы, тоже не случаен. Никто не знает, что такое фазовый сдвиг постоянного сигнала.
Выход фильтра имеет временную задержку. Чтобы относительный фазовый сдвиг входа и выхода был 90°, вход нужно задерживать на numtaps//2 сэмплов. Сделать это можно, дописав numtaps//2 нулей в начале последовательности сэмплов. Это еще одна причина, почему в преобразовании Гильберта используют нечетное количество коэффициентов. Когда оно четное, задержка фильтра составляет нецелое число сэмплов.
Аргументы метода remez() задают АЧХ фильтра. При желании можно получить ФВЧ, ДПФ, и так далее с фазовым сдвигом 90°. В данном примере во всей полосе [ 0 , nyq_rate ] фильтр обладает единичным усилением [ 1 ] .
Тот же фильтр может быть рассчитан и без remez() :
window = signal . windows . kaiser ( numtaps , beta = 8 )
taps = [ ( 1 / ( np. pi *n ) ) * ( 1 — np. cos ( np. pi *n ) )
for n in range ( 1 , ( numtaps// 2 ) + 1 ) ]
# an equivalent formula
# taps = [2*np.sin(np.pi*n/2)**2/(np.pi*n)
# for n in range(1, (numtaps//2)+1)]
# +90 deg phase shift
taps = np. append ( np. append ( np. flip ( taps ) , [ 0 ] ) , np. negative ( taps ) )
# -90 deg phase shift
# taps = np.append(np.negative(np.flip(taps)), np.append([0], taps))
taps = taps * window
Занимательный факт. Радиолюбители-конструкторы вместо фазовых сдвигов 0° и 90° часто используют пару фильтров со сдвигами +45° и −45°. Данный подход вычислительно неэффективен. Если вам все же нужен фазовый сдвиг на 45°, его можно получить, сложив сигнал с ним же, сдвинутым на 90°. По тому же принципу получаются любые другие фазовые сдвиги.
Для расчета IIR фильтров SciPy предлагает два метода. Первый — это iirfilter() :
# iirdesign.py
# Aleksander Alekseev, 2023
# https://remontka.com/scipy-dsp-filter-design/
import numpy as np
from scipy import signal
import matplotlib . pyplot as plt
import matplotlib . patches as patches
sample_rate = 44100.0
nyq_rate = sample_rate / 2.0
# ========================================
# Create a Chebyshev band-pass IIR filter
b , a = signal . iirfilter ( 11 , [ 5000 , 15000 ] , fs = sample_rate , rp = 0.5 ,
btype = ‘band’ , ftype = ‘cheby1’ )
# ========================================
print ( «=== a ({}) ===» . format ( a. size ) )
for t in a:
print ( «{},» . format ( t ) )
print ( «=== b ({}) ===» . format ( b. size ) )
for t in b:
print ( «{},» . format ( t ) )
# Plot the impulse response
idx = np. arange ( 0 , 256 )
x = 1.0 * ( idx == 0 )
ir = signal . lfilter ( b , a , x )
plt. figure ( 1 )
plt. plot ( ir , ‘o-‘ , linewidth = 2 )
plt. title ( ‘Impulse response’ )
plt. grid ( True )
# Plot the frequency response
w , h = signal . freqz ( b , a )
plt. figure ( 2 )
plt. title ( ‘Magnitude Response’ )
plt. plot ( ( w/np. pi ) *nyq_rate , 20 * np. log10 ( abs ( h ) ) , linewidth = 2 )
plt. ylabel ( ‘Amplitude [dB]’ )
plt. xlabel ( ‘Frequency’ )
plt. grid ( True )
plt. ylim ( — 95 , 5 )
# Plot zeros and poles
zeros , poles , _ = signal . tf2zpk ( b , a )
for m in np. abs ( poles ) :
if m >= 1.0 :
print ( «IIR FILTER IS UNSTABLE!» )
break
circle = patches. Circle (
( 0 , 0 ) , radius = 1 , fill = False ,
color = ‘black’ , ls = ‘solid’ , alpha = 0.3 )
fig , ax = plt. subplots ( )
plt. title ( ‘Poles and Zeroes’ )
ax. add_patch ( circle )
plt. plot ( zeros. real , zeros. imag , ‘o’ , markersize = 5 ,
alpha = 0.7 , label = «Zeros» )
plt. plot ( poles. real , poles. imag , ‘x’ , markersize = 5 ,
alpha = 0.7 , label = «Poles» )
plt. legend ( loc = ‘upper right’ )
plt. show ( )
Здесь мы рассчитываем фильтр Чебышева с полосой пропускания 5 кГц .. 15 кГц и рябью в полосе пропускания 0.5 dB:
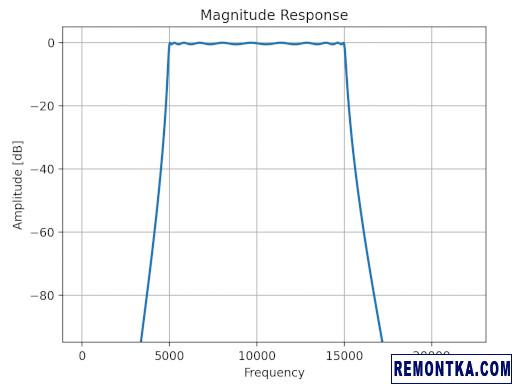
Проверить стабильность IIR фильтра можно двумя способами. Во-первых, подать единичный импульс и посмотреть на выход фильтра. Скрипт использует для этого метод lfilter() :
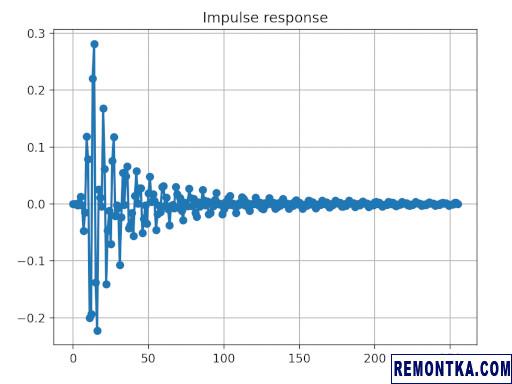
Фильтр не уходит в генерацию, а значит, стабилен.
Во-вторых, можно посмотреть, куда попадают нули и полюса. Метод iirfilter() возвращает передаточную функцию фильтра в области комплексных частот в формате коэффициентов полинома. Метод tf2zpk() переводит ее из формата коэффициентов полинома в формат корней многочлена, они же нули и полюса (исходный текст содержал ошибку, спасибо Kirill Kotyagin за уточнение):

Чтобы фильтр был стабильным, полюса должны находиться внутри единичного круга на комплексной плоскости. Если полюс попал прямо на круг или вышел за его пределы, значит фильтр нестабилен. Нули могут находиться где угодно. Их рисуют просто так, для красоты. Видим, что фильтр стабилен. В качестве эксперимента допишите в скрипт a [ 0 ] * = 1.003 и сравните результат.
Второй метод для расчета IIR фильтров — это iirdesign() :
b , a = signal . iirdesign ( wp = 9000 , ws = 11000 , fs = sample_rate ,
gpass = 1 , gstop = 60 )
# …
Здесь рассчитывается ФНЧ с полосой пропускания 9 кГц, подавлением 60+ dB выше 11 кГц и потерями в полосе пропускания не более 1 dB. Данный метод удобен тем, что сам определяет требуемое количество коэффициентов. Их здесь получилось 16 штук. FIR фильтру для достижения схожей АЧХ требуется порядка 60 .. 80 коэффициентов. Данный IIR фильтр стабилен, как и предыдущий.
Таким образом, мы установили, что SciPy действительно имеет все необходимое для расчета DSP фильтров.