Круговая диаграмма полных сопротивлений, она же диаграмма Вольперта-Смита или диаграмма Смита — это круговая диаграмма, часто используемая для отображения комплексного сопротивления чего бы то ни было. Одно из интересных свойств данной диаграммы заключается в том, что с ее помощью легко производить некоторые вычисления прямо на бумаге. Например, зная входное сопротивление антенны и рабочую частоту, нетрудно определить, как с помощью LC-схемы привести сопротивление к значению 50 Ом. Этим активно пользовались до появления персональных компьютеров, благодаря чему диаграмма Смита и обрела популярность. Давайте же попробуем порисовать диаграммы Смита на языке Python .
Для этого воспользуемся библиотекой pySmithPlot . Она в свою очередь зависит от Matplotlib и NumPy , про которые ранее уже рассказывалось в этом блоге. Чтобы не засорять систему кучей пакетов, воспользуемся virtualenv .
Итак, установка:
Здесь указана конкретная версия NumPy. На момент написания статьи у pySmithPlot была небольшая проблема с совместимостью с более поздними версиями. Имеется патч , но он еще не принят в апстрим. Вы можете использовать pySmithPlot с последней версией NumPy, но библиотеку придется скопировать в репозиторий вашего проекта и вручную применить патч.
Давайте сразу рассмотрим небольшую задачку. В рамках статьи Фильтры из коаксиального кабеля, часть 2 мы выяснили, как зависит входное сопротивление, которое мы видим на конце кабеля с волновым сопротивлением Z 0 , соединенного на втором конце с нагрузкой с сопротивлением Z L , от длины кабеля L:
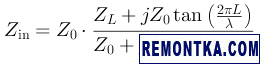
Здесь L измеряется в длинах волны λ. Естественно, в общем случае необходимо учитывать коэффициент укорочения кабеля. Так вот, допустим, мы используем кабель RG-6U+CU c Z 0 = 75 Ом, и он соединен с антенной delta loop , имеющей Z L = 106 Ом. Требуется изобразить на диаграмме Смита, как будет меняться Z in на интервале L ∈ [0; λ/4].
Решение:
import numpy as np
from math import pi , tan
from matplotlib import pyplot as pp
from smithplot import SmithAxes
def zf ( x ) :
z0 = 75
zl = 106
return z0* ( zl+1j*z0*tan ( x ) ) / ( z0+1j*zl*tan ( x ) )
pp. figure ( figsize = ( 6 , 6 ) )
ax = pp. subplot ( 1 , 1 , 1 , projection = ‘smith’ )
ax. update_scParams ( axes_impedance = 50 )
lam = np. linspace ( 0.0 , 0.25 , 8 )
imp = np. vectorize ( zf ) ( 2 *pi*lam )
pp. plot ( imp , datatype = «Z» )
pp. savefig ( ‘./smith.png’ )
А вот так выглядит картинка на выходе:
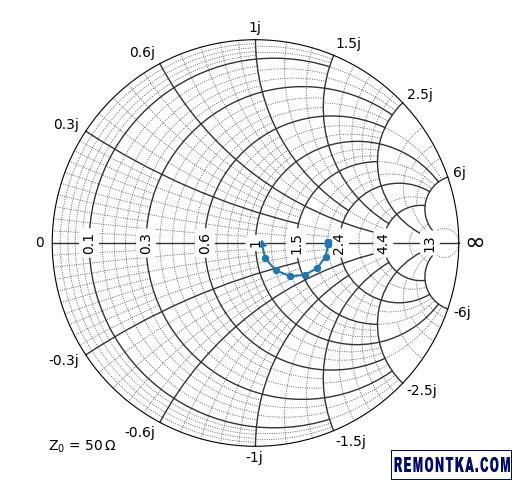
Видим, что при длине λ/4 кабель согласует 106 Ом антенны в почти идеальные 50 Ом, как и положенно четвертьволновому трансформатору.
Fun fact! Приведенная картинка наглядно иллюстрирует, почему балуны, использующие бифилярную обмотку , превосходно работают. Хотя, казалось бы, при использовании в балуне двухпроводной линии с волновым сопротивлением 150-300 Ом ничего хорошего ожидать не приходится. Если нагрузить такой балун на эквивалент нагрузки 50 Ом , то на условных 14 МГц мы действительно увидем КСВ 2. Однако ничто не мешает слегка подогнать размеры антенны, сделав ее входное сопротивление чуть-чуть реактивным. Отрезок двухпроводной линии в балуне преобразует это сопротивление в чисто активное, и антенна будет работать как надо. Заинтересованным читателям предлагается построить соответствующую диаграмму самостоятельно.
Это все, о чем я хотел сегодня рассказать. Больше примеров использования pySmithPlot вы найдете в репозитории проекта . Для желающих узнать больше о диаграммах Смита могу порекомендовать видео Basics of the Smith Chart , которое снял Alan Wolke, W2AEW.
Дополнение: Вас также могут заинтересовать посты Анализ антенного тюнера при помощи Python и Моделирование антенн на Python при помощи PyNEC .