NEC2++ — это движок для моделирования антенн, совместимый с NEC2. Движок написан на C++ и распространяется под лицензией GPL. Также предусмотрены байндинги к языку Python . О них далее и пойдет речь.
Для экспериментов нам понадобятся следующие пакеты:
Во избежание конфликтов между пакетами и чтобы не засорять систему, рекомендую использовать virtualenv . PyNEC указан конкретной версии по той причине, что в самой последней версии на момент написания статьи был открытый баг . Он делал использование пакета невозможным. К моменту, когда вы будете читать эти строки, баг может быть устранен.
Моделировать будем антенну inverted-V на диапазон 20 метров, установленную на 10-и метровой мачте. У нас будет несколько скриптов, анализирующих разные свойства антенны. Общий код положим в файл common.py:
from math import pi , sin
def free_space ( nec ) :
# 0 — no ground plane
# 1 — ground plane with current expansion
# -1 — ground plane without current expansion
nec. geometry_complete ( 0 )
def good_ground ( nec ) :
conductivity = 0.0303 # S/m
rel_dielectric_constant = 20.0
nec. geometry_complete ( 1 )
nec. gn_card ( 0 , 0 , rel_dielectric_constant , conductivity ,
0 , 0 , 0 , 0 )
def average_ground ( nec ) :
conductivity = 0.005 # S/m
rel_dielectric_constant = 13.0
nec. geometry_complete ( 1 )
nec. gn_card ( 0 , 0 , rel_dielectric_constant , conductivity ,
0 , 0 , 0 , 0 )
def poor_ground ( nec ) :
conductivity = 0.001 # S/m
rel_dielectric_constant = 3.0
nec. geometry_complete ( 1 )
nec. gn_card ( 0 , 0 , rel_dielectric_constant , conductivity ,
0 , 0 , 0 , 0 )
def geometry ( length = 5.22 , angle = 100 , height = 10 , nr_segments = 21 ,
ground = average_ground ) :
nec = PyNEC. nec_context ( )
nec. set_extended_thin_wire_kernel ( False )
wire_radius = 0.0005 # 0.5 mm
length_ratio = 1.0
radius_ratio = 1.0
eps = 0.1
b = length*sin ( pi*angle/ 2 / 180 )
a = length*sin ( pi* ( 90 — angle/ 2 ) / 180 )
geo = nec. get_geometry ( )
# center
geo. wire ( 1 , 1 , 0 , -eps , height , 0 , eps , height ,
wire_radius , length_ratio , radius_ratio )
# left
geo. wire ( 2 , nr_segments , 0 , -b , height-a , 0 , -eps , height ,
wire_radius , length_ratio , radius_ratio )
# right
geo. wire ( 3 , nr_segments , 0 , b , height-a , 0 , eps , height ,
wire_radius , length_ratio , radius_ratio )
ground ( nec )
# voltage excitation in the center of the antenna
segment_nr = 1
voltage = 1.0 +0j
ex_voltage_excitation = 0
nec. ex_card ( ex_voltage_excitation , segment_nr , 1 , 1 ,
voltage. real , voltage. imag , 0 , 0 , 0 , 0 )
return nec
Здесь основная функция — это geometry . Она возвращает объект nec_context. Объект имеет N-ое количество методов-оберток к движку, а также хранит стейт с информацией о свойствах земли, проводах, из которых состоит антенна, и что именно в ней нужно промоделировать.
Не могут не бросаться в глаза странные имена методов, вроде gn_card и ex_card . Эта терминология позаимствована из движка NEC2. Движок принимает на вход файл, содержащий строки в определенном формате. Файл в терминологии NEC2 называется колодой (deck), а строки в нем — картами (card). Нужно понимать, что история NEC2 уходит корнями во времена, когда программисты писали на Fortran и работали с перфокартами. Отсюда и такая терминология.
Так вот, допустим, мы хотим описать землю. Для этого в файл нужно добавить строчку GN (какие-то аргументы) . Говорят, что это GN-карта. Описание всех возможных карт, ровно как и их аргументов, можно найти в документации на NEC2 . Пример колоды есть на Википедии . Еще в cocoaNEC можно открыть вкладку «Cards» и посмотреть, в какую колоду был странслирован код на NC.
Обладая этой информацией, код перестает казаться таким уж запутанным. Здесь мы объявили четыре варианта земли. Аргументы для GN-карт были банально подсмотрены в cocoaNEC. Далее в функции geometry мы рисуем inverted-V из трех проводов ( geo. wire ), подстилаем под ними землю, и говорим, что антенна питается в первый сегмент провода с меткой «1» ( nec. ex_card ).
Имея модель антенны, какая идея первой приходит на ум? Конечно же, построить график КСВ:
import matplotlib . pyplot as plt
import PyNEC
from common import *
def vswr ( z , z0 ) :
Gamma = abs ( ( z — z0 ) / ( z + z0 ) )
return float ( ( 1 + Gamma ) / ( 1 — Gamma ) )
nec = geometry ( )
system_impedance = 50
count = 100
start_freq = 13.8
stop_freq = 14.6
step_size = ( stop_freq — start_freq ) / count
ifrq_linear_step = 0
nec. fr_card ( ifrq_linear_step , count , start_freq , step_size )
nec. xq_card ( 0 ) # execute simulation
freqs = [ ]
vswrs = [ ]
for idx in range ( 0 , count ) :
ipt = nec. get_input_parameters ( idx )
z = ipt. get_impedance ( )
freqs. append ( ipt. get_frequency ( ) / 1000000 )
vswrs. append ( vswr ( z , system_impedance ) )
dpi = 80
plt. figure ( dpi = dpi , figsize = ( 512 / dpi , 384 / dpi ) )
plt. plot ( freqs , vswrs )
plt. title ( «SWR vs Frequency» )
plt. xlabel ( «Frequency, MHz» )
plt. ylabel ( «SWR» )
plt. axis ( [ start_freq , stop_freq , 1.0 , 3.0 ] )
plt. grid ( True )
plt. savefig ( «swr.png» )
Здесь FR-карта задает интервал частот, на котором будет анализироваться антенна, а XQ-карта запускает моделирование. В итоге мы получаем данные для 100 частот с шагом 8 кГц. Для каждой частоты определяется входное сопротивление антенны. Из него вычисляется КСВ, график которого нам и нужен. График рисуется при помощи библиотеки Matplotlib .
Результат:
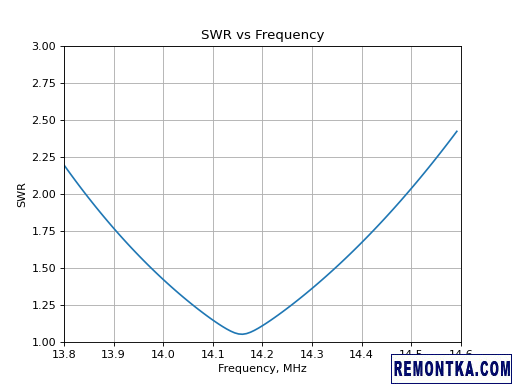
С тем же успехом входное сопротивление антенны можно отобразить на диаграмме Вольперта-Смита . Заинтересованным читателям предлагается модифицировать скрипт соответствующим образом в качестве упражнения.
Казалось бы, на КСВ можно остановиться, но уж нет! Раз есть модель антенны, то нарисуем полярную диаграмму ее усиления под углом 33° к горизонту на середине телеграфного участка:
import matplotlib . pyplot as plt
import PyNEC
from common import *
nec = geometry ( )
freq_mhz = 14.035
ifrq_linear_step = 0
nec. fr_card ( ifrq_linear_step , 1 , freq_mhz , 0 )
elevation = 33
theta_angle = 90 — elevation
nec. rp_card ( calc_mode = 0 , n_theta = 1 , n_phi = 360 ,
output_format = 1 , normalization = 0 , D = 0 , A = 0 , # XNDA = 1000
theta0 = theta_angle , phi0 = 0 , delta_theta = 0 , delta_phi = 1 ,
radial_distance = 5000 , gain_norm = 0 )
nec. xq_card ( 0 ) # execute simulation
rpt = nec. get_radiation_pattern ( 0 )
gain = rpt. get_gain_tot ( )
gm = max ( gain )
xs = [ 2 *pi* float ( phi ) / 360 for phi in range ( gain. size ) ]
ys = [ — 36 if g-gm < — 36 else g-gm for g in gain ]
dpi = 80
fig = plt. figure ( dpi = dpi , figsize = ( 512 / dpi , 384 / dpi ) )
ax = plt. subplot ( 111 , projection = ‘polar’ )
ax. set_title ( ‘Elevation {} deg’ . format ( elevation ) )
ax. set_xlabel ( ‘Max gain: {:.2f} dBi’ . format ( gm ) )
ax. plot ( xs , ys , linestyle = ‘solid’ , color = ‘red’ )
ax. set_rmax ( 0 )
ax. set_rticks ( [ — 6 *i for i in range ( 0 , 7 ) ] )
ax. set_yticklabels ( [ » ] + [ str ( — 6 *i ) for i in range ( 1 , 7 ) ] )
ax. set_theta_direction ( — 1 )
ax. set_rlabel_position ( — 90 )
ax. set_thetagrids ( range ( 0 , 360 , 15 ) )
ax. grid ( True )
fig. savefig ( ‘elevation.png’ )
FR-карта в этот раз задает одну, фиксированную частоту. За диаграмму направленности отвечает RP-карта . В этой карте нужно указать начальные значения углов phi и theta в сферической системе координат , с каким шагом и сколько раз они будут обновляться, плюс некоторые другие параметры. Заметьте, что зениту соответствует theta = 0 . В итоге для всех пар (phi, theta) получаем усиление антенны в dBi. Его остается только отобразить на полярной диаграмме. Сталкиваться с последней нам уже доводилось :
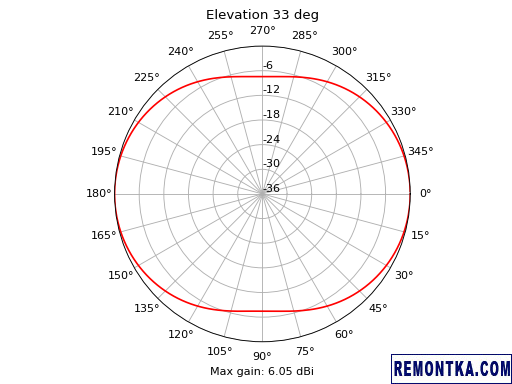
И для полноты картины построим аналогичную диаграмму для фиксированного азимута и переменной элевации:
import matplotlib . pyplot as plt
import PyNEC
from common import *
nec = geometry ( )
freq_mhz = 14.035
ifrq_linear_step = 0
nec. fr_card ( ifrq_linear_step , 1 , freq_mhz , 0 )
azimuth = 0
nec. rp_card ( calc_mode = 0 , n_theta = 181 , n_phi = 1 ,
output_format = 1 , normalization = 0 , D = 0 , A = 0 , # XNDA = 1000
theta0 = — 90 , phi0 = azimuth , delta_theta = 1 , delta_phi = 0 ,
radial_distance = 5000 , gain_norm = 0 )
nec. xq_card ( 0 ) # execute simulation
rpt = nec. get_radiation_pattern ( 0 )
gain = rpt. get_gain_tot ( )
gm = max ( gain )
xs = [ 2 *pi* float ( 90 -theta ) / 360 for theta in range ( gain. size ) ]
ys = [ — 36 if g-gm < — 36 else g-gm for g in gain ]
dpi = 80
fig = plt. figure ( dpi = dpi , figsize = ( 512 / dpi , 384 / dpi ) )
ax = plt. subplot ( 111 , projection = ‘polar’ )
ax. set_title ( ‘Azimuth {} deg’ . format ( azimuth ) )
ax. set_xlabel ( ‘Max gain: {:.2f} dBi’ . format ( gm ) )
ax. set_thetamin ( — 90 ) # set the limits
ax. set_thetamax ( 90 )
ax. set_theta_offset ( 2 *pi* 90 / 360 )
ax. plot ( xs , ys , linestyle = ‘solid’ , color = ‘red’ )
ax. set_rmax ( 0 )
ax. set_rticks ( [ — 6 *i for i in range ( 0 , 7 ) ] )
ax. set_yticklabels ( [ » ] + [ str ( — 6 *i ) for i in range ( 1 , 7 ) ] )
ax. set_thetagrids ( range ( — 90 , 91 , 15 ) )
ax. set_theta_direction ( — 1 )
ax. grid ( True )
fig. savefig ( ‘azimuth.png’ )
Результат:

Диаграмма выглядит немного непривычно. Дело в том, что масштаб на ней, как и на предыдущей диаграмме, линейный. Но в книгах и в антенных моделировщиках мы привыкли видеть логарифмический масштаб. Заинтересованным читателям предлагается устранить этот дефект в качестве упражнения. Также в качестве упражнения предлагается нарисовать диаграмму направленности антенны в 3D. Полную версию исходников вы найдете на GitHub .
При помощи PyNEC могут быть решены разные задачи. Например, его можно использовать для оптимизации антенн по заданному критерию. Кроме того, библиотека может послужить основой для кроссплатформенного антенного моделировщика.
Дополнение: Пример практического применения PyNEC описан в заметке Антенна ZS6BKW на пять КВ-диапазонов .