В этой статье мы поведем речь о таких параметрах, как активное и реактивное сопротивление.

Активное сопротивление

И начнем мы статью не с реактивного сопротивления, как ни странно, а с простого и всеми нами любимого радиоэлемента  — резистора , который, как говорят, обладает активным сопротивлением . Еще иногда его называют омическим .  Как нам говорит вики-словарь, «активный  — это деятельный, энергичный, проявляющий инициативу». Активист готов всегда рвать и метать даже ночью. Он готов ПОЛНОСТЬЮ выложиться и потратить всю энергию во благо общества.

То же самое можно сказать и про другие нагрузки, обладающие активным сопротивлением. Это могут быть различные нагревательные элементы, типа тэнов, а также лампы накаливания.

Как смотреть силу тока в цепи через осциллограф

Чем же резистор отличается от катушки индуктивности и конденсатора ? Понятное дело, что выполняемыми функциями, но этим все не ограничивается. Итак, давайте рассмотрим самую простую схемку во всей электронике:

На схеме мы видим генератор частоты и резистор.

Давайте визуально посмотрим, что у нас творится в этой схеме. Для этого, как я уже сказал, нам понадобится генератор частоты

А также цифровой осциллограф :

С помощью него мы будем смотреть напряжение и силу тока .

Что?

Силу тока?

Но ведь осциллограф предназначен для того, чтобы рассматривать форму сигнала напряжения? Как же мы будем рассматривать форму сигнала силы тока? А все оказывается просто). Для этого достаточно вспомнить правило шунта .

Кто не помнит —  напомню. Имеем обыкновенный резистор:

Что будет, если через него прогнать электрический ток ?

100 Герц

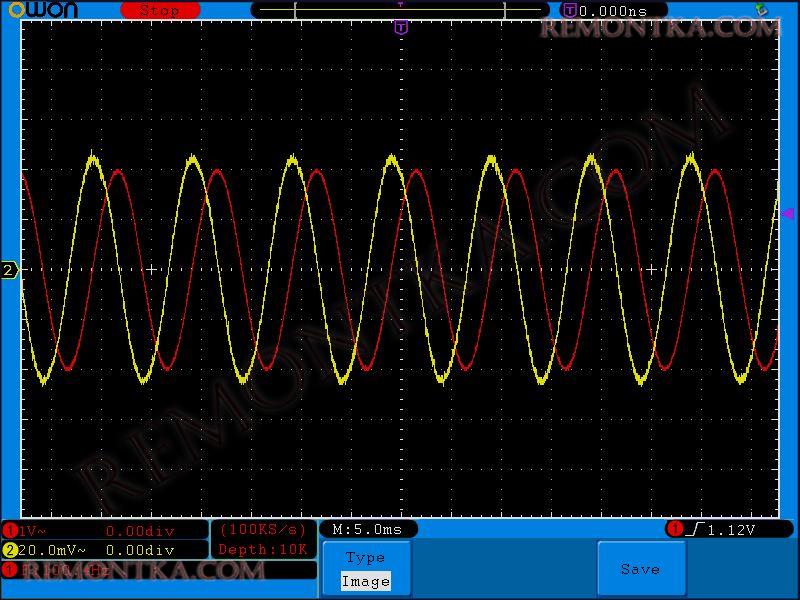
200 Герц

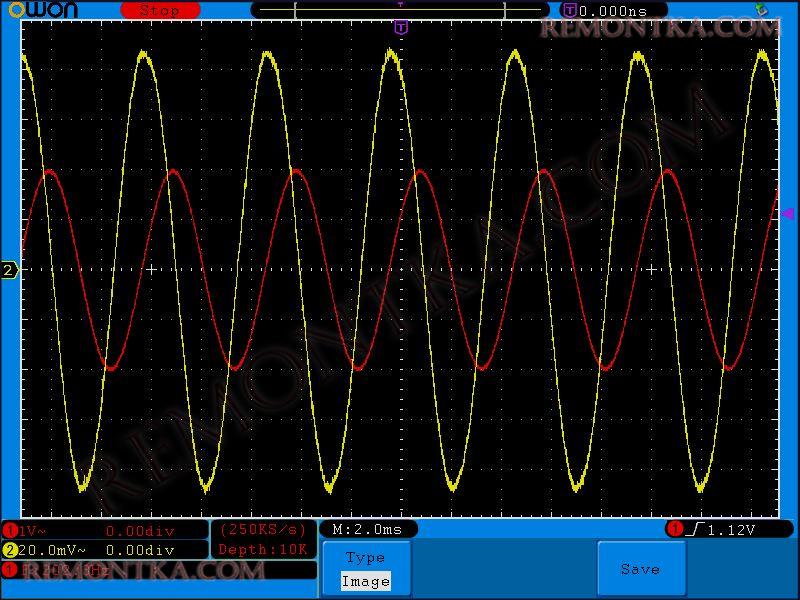
Как вы видите, с увеличением частоты, у нас сила тока в цепи с конденсатором возрастает.

Реактивное сопротивление конденсатора

Как мы увидели с прошлого опыта, с увеличением частоты растет сила тока! Кстати, у резистора не росла. То есть получается в данном случае из закона Ома, что сопротивление конденсатора зависит от частоты! Да, все так оно и есть. Но называется оно не просто сопротивлением, а реактивным сопротивлением и вычисляется по формуле:

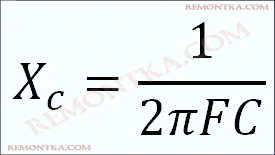
где

Х _с — реактивное сопротивление конденсатора, Ом

П — постоянная и приблизительно равна 3,14

F — частота, Гц

С — емкость конденсатора, Фарад

Катушка индуктивности в цепи переменного тока

Ну а теперь давайте возьмем катушку индуктивности вместо конденсатора:

Проводим все аналогичные операции, как и с конденсатором. Смотрим на осциллограммы в цепи с катушкой индуктивности:

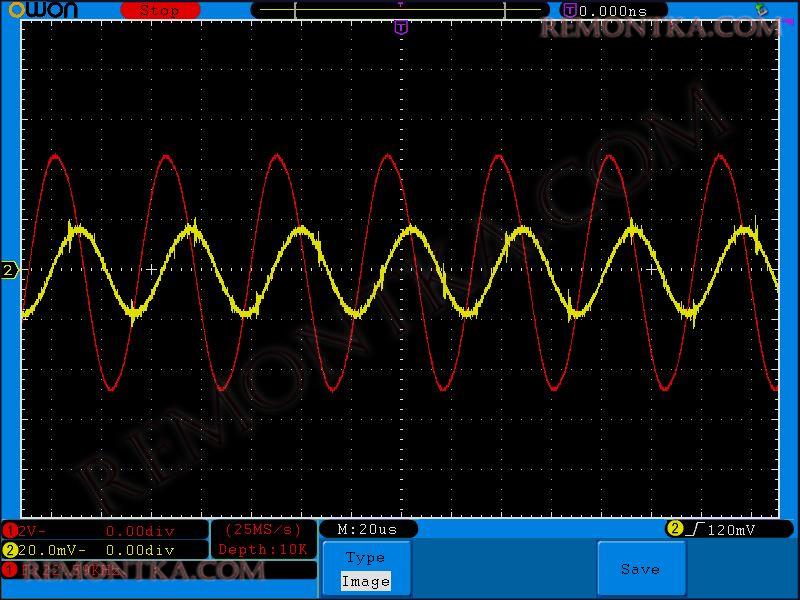
Если помните, вот такую осциллограмму мы получили в схеме с конденсатором:

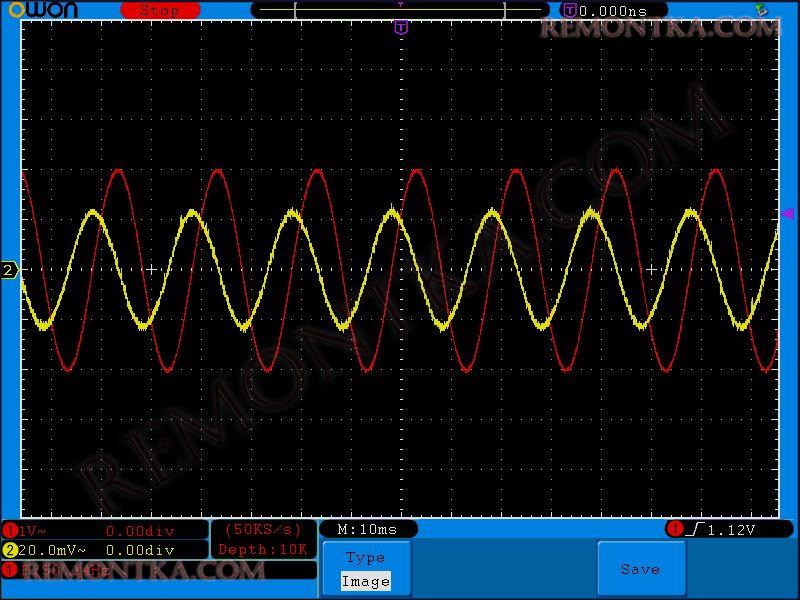
Видите разницу? На катушке индуктивности ток отстает от напряжения на  90 градусов, на П/2, или, как еще говорят, на четверть периода (весь период у нас 2П или 360 градусов).

Так-так-так…. Давайте соберемся с мыслями. То есть в цепи с переменным синусоидальным током,  ток на конденсаторе опережает напряжение на 90 градусов, а на катушке индуктивности ток отстает от напряжения тоже на 90 градусов? Да, все верно.

Почему на катушке ток отстает от напряжения?

Не будем углубляться в различные физические процессы и формулы, просто сочтем за данность, что сила тока не может резко возрастать на катушке индуктивности. Для этого проведем простой опыт. Так же как и на конденсатор, мы резко подадим напряжение на катушку индуктивности, и посмотрим, что случилось с силой тока.

Как вы видите, при резкой подаче напряжения на катушку, сила тока не стремится также резко возрастать, а возрастает постепенно, если быть точнее, по экспоненте.

Давайте вспомним, как это было у конденсатора:

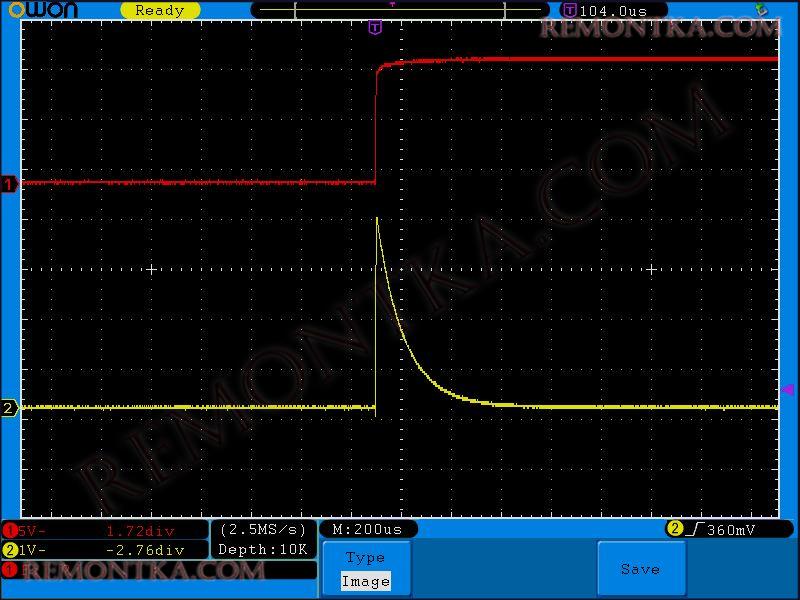
Все с точностью наоборот! Можно даже сказать, что катушка — это полная противоположность конденсатору 😉

Ну и напоследок давайте еще побалуемся частотой:

240 Килогерц

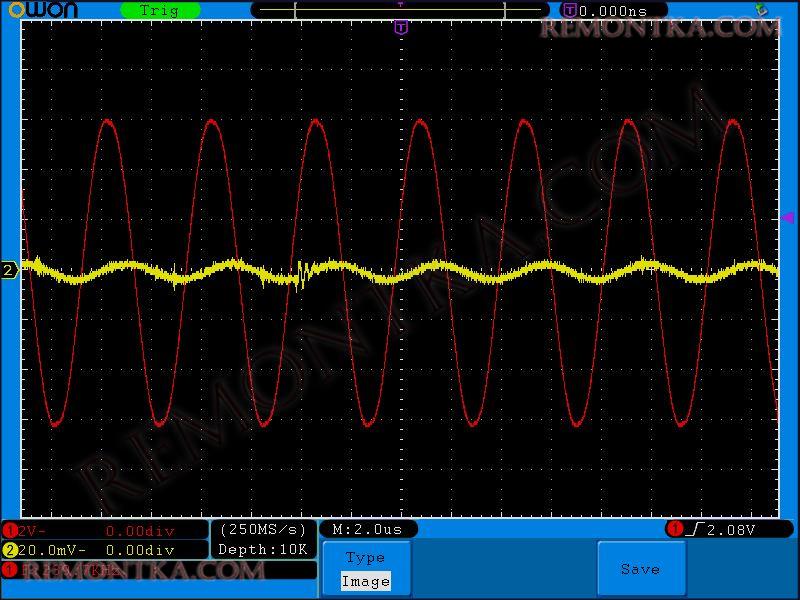
34 Килогерца

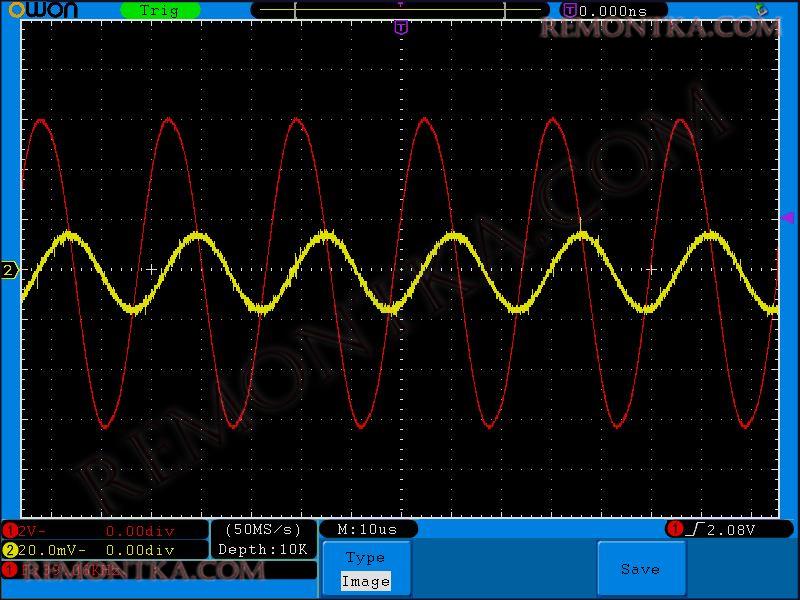
17 Килогерц

10 Килогерц

Вывод?

С уменьшением частоты сила тока через катушку увеличивается.

Реактивное сопротивление катушки индуктивности

Из опыта выше мы можем сделать вывод, что сопротивление катушки зависит от частоты и вычисляется по формуле

где

Х _L —  реактивное сопротивление катушки, Ом

П — постоянная и приблизительно равна 3,14

F — частота, Гц

L — индуктивность , Генри

Мощность в цепи с реактивными радиоэлементами

Для дальнейшего объяснения этого явления нам потребуется наша осциллограмма с катушки индуктивности:

Итак, давайте выделим на ней один период и разделим его на 4 части, то есть по 90 градусов каждая или π /2 .

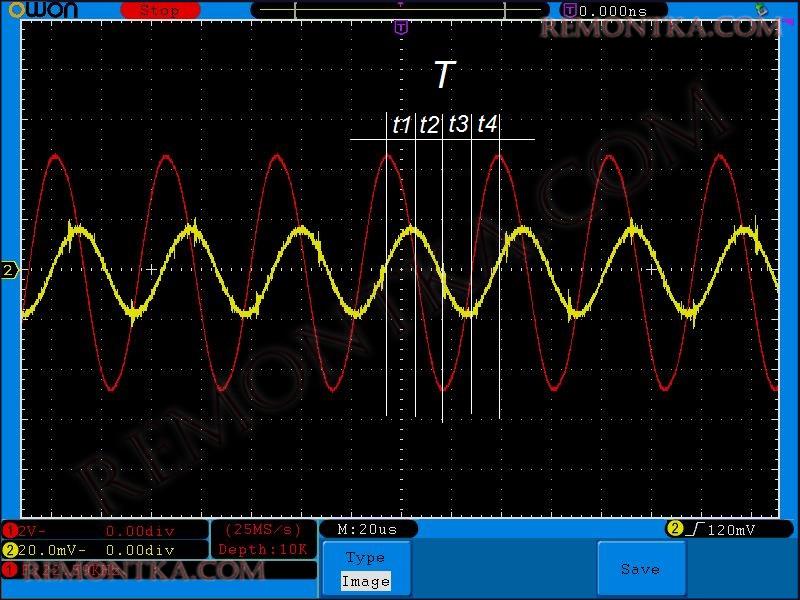
Давайте начнем с такого понятия, как мощность. Если не забыли, мощность — это сила тока помноженное на напряжение, то есть P=IU . Итак, в первую четвертинку периода t1 у нас напряжение принимает положительные значения и сила тока тоже положительное. Плюс на плюс дает плюс. В эту четверть периода энергия поступает из источника в реактивное сопротивление.

Теперь давайте рассмотрим отрезок времени t2 . Здесь ток со знаком «плюс», а напряжение со знаком «минус». В итоге плюс на минус дает минус. Получается мощность со знаком «минус». А разве так бывает? Еще как бывает! В этот промежуток времени реактивный радиоэлемент отдает запасенную энергию обратно в источник напряжения. Для лучшего понимания давайте рассмотрим простой житейский пример.

Представим себе кузнеца за работой:

Не знаю, какое было у вас детство, но я когда был пацаном, брал свинец с аккумуляторов и плющил его в металлические пластинки. И что думаете? Свинец нагревался. Не так, чтобы прям обжигал, а был тепленький на ощупь. То есть моя энергия удара превращалась в тепло, можно даже сказать, в полезную энергию.

А что если взять пружину от стоек ВАЗа и ударять по ней?

С пружиной не станет НИ-ЧЕ-ГО! Она ведь не свинец. Но… заметьте вот такую вещь: как только мы начинаем «плющить» пружину кувалдой, у нас она начинает сжиматься. И вот она сжалась до упора и… выстрелила вверх, подхватив с собой тяжелую кувалду, которая только что пыталась ее расплющить. То есть в данном случае энергия вернулась обратно в источник энергии, то есть обратно  к кузнецу. Он вроде как и пытался расплющить пружину, но пружина вернула энергию обратно своим разжатием. То есть кузнецу не надо уже было подымать тяжелый молот, так как за него это уже сделала пружина.

Разжатие пружины и возврат ею энергии обратно — это и есть отрицательная мощность. В этом случае энергия возвращается обратно в источник. Хорошо ли это или плохо — это уже другая история.

В третий промежуток времени t3 и ток и напряжение у нас со знаком «минус». Минус на минус — это плюс. То есть реактивный элемент снова поглощает энергию, ну а на t4 , снова ее отдает, так как плюс на минус дает минус.

В результате за весь период у нас суммарное потребление энергии равно чему?

Правильно, нулю!

Так что же это получается тогда? На катушке и конденсаторе не будет выделяться никакой энергии? Получается так. Поэтому в схемах они чаще всего холодные, хотя могут быть и слегка теплыми, так как реальные параметры катушки и конденсатора выглядят совсем по другому.

Эквивалентная схема реальной катушки индуктивности выглядит вот так:

где

R _L — это сопротивление потерь. Это могут быть потери в проводах, так как любой провод обладает сопротивлением. Это могут быть потери в диэлектрике, потери в сердечнике и потери на вихревые токи.  Как видите, раз есть сопротивление, значит на нем может выделяться мощность, то есть тепло.

L — собственно сама индуктивность катушки

С — межвитковая емкость.

А вот и эквивалентная схема реального конденсатора:

где

r — сопротивление диэлектрика и корпуса между обкладками

С — собственно сама емкость конденсатора

ESR — эквивалентное последовательное сопротивление

ESI (ESL) — эквивалентная последовательная индуктивность

Здесь мы тоже видим такие параметры, как r  и ESR, которые на высоких частотах будут еще лучше себя проявлять, благодаря скин-эффекту. Ну и, соответственно, на них будет выделяться мощность, что приведет к небольшому малозаметному нагреву.

Резюме

Резистор обладает активным (омическим) сопротивлением. Катушка индуктивности и конденсатор обладают реактивным сопротивлением.

В цепи переменного тока на конденсаторе ток опережает напряжение на 90 градусов, а на катушке ток отстает от напряжения на 90 градусов.

Сопротивление катушки вычисляется по формуле

Сопротивление конденсатора вычисляется по формуле:

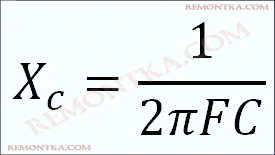
В цепи переменного тока на идеальном реактивном сопротивлении не выделяется мощность.

Реальные катушка и конденсатор имеют в своем составе паразитные параметры, которые имеют некоторое сопротивление. Поэтому реальные катушка и конденсатор не обладают чисто реактивным сопротивлением.