В последнее время я несколько раз упоминал о том, что не совсем понимаю, как на Haskell можно разрабатывать настоящие, большие проекты. Тому было несколько причин, но главным образом меня беспокоило (заметьте, в прошедшем времени), что Haskell активно использует ленивые вычисления. Тут имеет место серьезная проблема, о которой обычно умалчивают евангелисты и которую плохо осознаешь в начале изучения этого языка.

Вспомним, чем хороши ленивые вычисления:

• Они позволяют использовать в наших программах разные интересные вещи, например, бесконечные списки и завязывание в узел;
• То, что не нужно, никогда не вычисляется. За счет этого получаем б о льшую производительность . Существенно упрощается реализация эффективных чисто функциональных алгоритмов и структур данных;
• Ленивые вычисления могут приводить и к экономии оперативной памяти. Если для обработки пользовательского запроса нужно построить только 42% какого-нибудь бинарного дерева, будут построены только эти 42%;
• В некоторых случаях получаем мемоизацию из коробки;

Есть и другие маленькие приятные моменты. Например, в некоторых случаях ленивые вычисления избавляют нас от необходимости переписывать функции с использованием хвостовой рекурсии. Вроде, я ничего не забыл.

Если вы помедитируете достаточно большое количество времени над этим вопросом, то обнаружите, что ленивые вычисления — это такая же мощная и полезная часть языка, как, например, правильно реализованные легковесные процессы или автоматическая сборка мусора. Как и в случае с легковесными процессами, польза от ленивых вычислений не так уж очевидна, если вы занимаетесь исключительно задачами типа «сходить в базу, сгенерить JSON». Хотя, при желании, им и там найдется пара применений. Куда более ценными ленивые вычисления становятся, если вы, скажем, пишите компилятор .

Например, вы можете написать семантический анализатор, который использует результат синтаксического анализа (лениво), который в свою очередь использует результат лексического анализа. При этом, если выяснится, что в десятой строке программа имеет семантическую ошибку, вы можете сразу завершить анализ. При этом будет потрачено время и оперативная память, необходимые только для выявления этой ошибки. А теперь представьте, сколько работы нужно сделать, чтобы скомпоновать компоненты системы таким образом в каком-нибудь Си.

Так о какой «серьезной проблеме» идет речь? Рассмотрим следующую программу:

Скомпилировав и запустив ее следующим образом:

… мы увидим занятное сообщение:

Многовато для такой простой программы, не так ли? Подумав немного, мы замечаем, что в функции mysum не используется хвостовая рекурсия. Переписываем программу:

Запускаем аналогичным образом:

Что же случилось? Почему с хвостовой рекурсией программа стала использовать не меньше оперативной памяти, а даже больше? Будучи ленивым языком, Haskell откладывает вычисление аргументов функций до последнего момента. Вместо того, чтобы сразу вычислять значение аккумулятора на каждом шаге рекурсии, Haskell передает невычисленное значение (thunk) «0+1», затем «0+1+2» и так далее, в результате чего расходуется оперативная память. Аккумулятор вычисляется только на последнем шаге рекурсии.

С этой проблемой можно бороться разными способами. Например, при помощи функции seq :

В первом приближении, она вычисляет свой первый аргумент, как это было бы сделано в строгом языке программирования, после чего возвращает свой второй аргумент. Таким образом, у нас появляется возможность использовать строгие вычисления вместо ленивых там, где это нужно:

В действительности, seq приводит свой первый аргумент к слабой головной нормальной форме (weak head normal form, WHNF). Отличие от нормальной формы (NF, иногда также называют reduced normal form, RNF), в которой данные вычислены полностью, состоит в том, что вычисление останавливается при достижении внешнего конструктора. Например, следующее выражение будет вычислено вполне успешно:

Для приведения выражения к нормальной форме можно воспользоваться функцией deepseq из одноименного пакета. Иногда можно встретить упоминание головной нормальной формы (head normal form, HNF). Отличие от WHNF состоит в следующем. HNF требует, чтобы тело лямда-функции было редуцировано, в то время, как WHNF этого не требует. Например, x -> 1 + 1 находится в WHNF, но не в HNF. Для обычных данных WHNF и HNF — одно и то же. Это в теории. На практике HNF не встречается в Haskell , поэтому имеет смысл говорить только о нормальной форме и слабой головной нормальной форме.

Дополнение: Зачем вообще нужен seq, когда есть deepseq? Дело в том, что seq отрабатывает за O(1), в то время, как deepseq — за O(N). Это несложно проверить в ghci для списка вроде [ x ^ 1000000 ` mod ` 100 | x <- [ 1 .. 100 ] ] .

Второй способ — использовать расширение BangPatterns компилятора GHC. В действительности, это всего лишь синтаксический сахар над seq :

Также мы можем прибегнуть к строгим вычислениям при помощи оператора ( $! ) :

Он работает аналогично оператору ( $ ) , за тем исключением, что аргумент функции приводятся к WHNF. В пакете deepseq есть оператор ( $!! ) , являющийся «глубоким» аналогом ( $! ) .

Наконец, Haskell позволяет объявлять строгие типы данных:

По умолчанию типы данных в Haskell являются ленивыми, однако мы можем изменить это при помощи приведенного выше синтаксиса. Здесь поля a и b будут приводится к WHNF. К слову, строгие аннотации являются частью стандарта Haskell, а не каким-нибудь расширением компилятора GHC.

Интересный момент. Если скомпилировать версию программы, в которой мы использовали хвостовую рекурсию (то есть, вторую по счету), с флагом -O2, она будет потреблять столько же памяти, сколько и оптимизированные версии. При использовании флага -On компилятор пытается найти аргументы функций, которые вычисляются всегда, а потому могут быть вычислены строго, а не лениво. Эта оптимизация называется «анализ строгости» (strictness analysis) .

Означает ли это, что можно писать на Haskell, думая о нем, как о строгом языке, а компилятор сам обо всем позаботится? К сожалению, нет. Следующий код без дополнительных телодвижений со стороны программиста съедает 10 Мб оперативной памяти даже при использовании флага -O2:

Здесь функция mysum считает сумму первых len элементов списка и возвращает пару из посчитанной суммы и оставшихся элементов списка. В данном случае компилятор не может принудительно вычислить acc, поскольку нет гарантий, что его значение будет использовано вызывающей функцией.

Выходит, из-за ленивых вычислений некоторые функции в нашей программе могут использовать лишнюю оперативную память. Есть ли способ обнаружить такие функции?

Для поиска «узких мест» в программах на Haskell следует использовать профайлер. Например, чтобы выяснить, какая функция сколько времени выполняется, скажем:

Если во время компиляции программы вы увидите такую ошибку:

… установите пакет haskell-platform-prof. Во всяком случае, так он называется у меня в Ubuntu.

В результате запуска программы будет создан текстовый файл sum.prof с информацией о том, какие функции сколько раз вызывались и какую часть от общего времени выполнения программы выполнялись. Но сейчас нас куда больше интересует память, а не скорость. Профайлер приходит на помощь и здесь:

Флаг -i задает частоту в секундах, с которой будет собираться статистика использования памяти. Чем меньше это значение, тем более точные данные мы получим, но и тем медленнее будет работать программа.

Будет создан файл sum.hp. Для его просмотра нам понадобится набор утилит hp2any . Под Ubuntu я устанавливал его примерно следующим образом:

На основе файла sum.hp можно сгенерировать картинку в формате PostScript:

Также можно воспользоваться GUI-программой Heap Profile Manager:

В последнем случае вы должны увидеть примерно следующее:

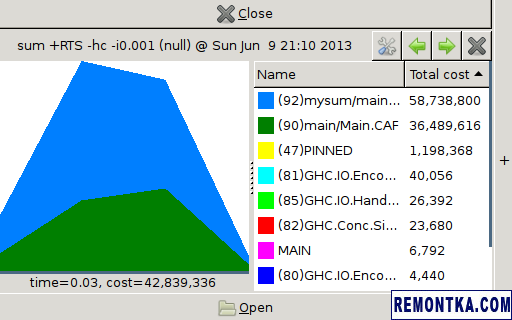
Функции можно сортировать по их «стоимости». При наведении мыши на определенный график в правой колонке подсвечивается функция, которой он соответствует. Совершенно очевидно, что б о льшая часть памяти была выделена внутри функции mysum.

Аналогичный отчет можно построить и для типов данных:

В результате получится такая картинка:

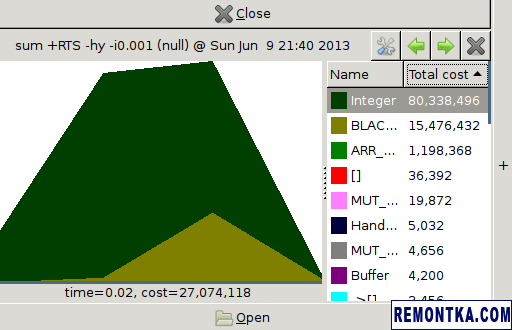
Благодаря ей легко видеть, что б о льшая часть памяти была выделена под данные типа Integer.

Итак, мы выяснили, что компилятор часто оказывается достаточно умен для того, чтобы самостоятельно использовать строгие вычисления вместо ленивых. В тех случаях, когда компилятор дает маху, мы можем обнаружить проблемные функции при помощи профайлера, а затем оптимизировать их. Благо, Haskell дает нам возможность выбирать между ленивыми вычислениями и строгими. Кстати, последнее как бы намекает, что Haskell, вообще-то говоря, не является ленивым языком программирования .

Я пришел к следующему выводу. В связи со сказанным выше, разработка на Haskell имеет свои нюансы. Нужно помнить о ленивых вычислениях, следить за используемым объемом памяти, и при возникновении проблем внимательно смотреть на последние изменения, внесенные в программу. Думаю, с этим можно жить. При программировании на Erlang я постоянно помню о динамической типизации , переполнении очередей сообщений и тд. Если же я пишу на Си , то думаю об освобождении ресурсов, переполнении буфера и арифметике над указателями. Всюду свои нюансы.

Материалы по теме:

• Глава о профалинге и оптимизации в «Real World Haskell»;
• Подробный пост на StackOverflow о профайлинге программ на Haskell ;
• Обсуждение различий между WHNF и HNF на том же StackOverflow;
• О том, что такое CAF и как долго Haskell хранит вычисленные санки , плюс пара полезных ссылок есть в комментарии к первому ответу;
• Несколько способов получить строгие вычисления в Haskell описаны в посте Мини заметки — выпуск 17, полностью посвященный Haskell ;
• EKG позволяет смотреть некоторые полезные метрики работающего приложения, а также умеет репортить их в StatsD ;
• Можно ограничить максимальный размер кучи программы с помощью флага системы выполнения -M — устанавливаем при прогоне тестов, если падают с OOM, значит в последнем коммите что-то было сделано не так;

Вопросы, замечания, дополнения, а также нажатия на кнопки социальных сетей, как обычно, горячо приветствуются!

Дополнение: Оказывается, в ghci есть команда :sprint, работающая как-то так:

Как видите, с ее помощью можно выяснить, вычислено ли некоторое выражение, или же мы имеем thunk.

Дополнение: Иногда также приводится аргумент, что ленивые вычисления дают модульность. Дескать, код take 5 $ sort просто находит 5 наименьших элементов, не сортируя список целиком. В строгих языках функции таким образом не компонуются, приходится писать дополнительный код. Однако здесь есть и контраргумент. Чтобы понимать, что такой код действительно эффективно находит 5 наименьших элементов, нужно знать, как реализована функция sort. И если функция sort, скажем, будет модифицирована так, что сначала она сортирует список по убыванию, а потом делает reverse, код take 5 $ sort уже перестанет быть эффективным. Получается противоречие — чтобы получить модульность, мы ломаем абстракцию, а следовательно и саму модульность , которую желали получить.