Делитель напряжения позволяет получить меньшее напряжение из большего, напряжение может быть как постоянным, так и переменным.
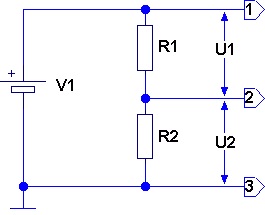
Рис. 1. Схема простейшего делителя напряжения
Простейшая схема делителя напряжения содержит минимум два сопротивления. Если величины сопротивлений одинаковы, то согласно закону Ома, на выходе делителя будет получено напряжение, в два раза меньшее, чем на входе, так как падение напряжений на резисторах будет одинаковым. Для других случаев величина падения напряжений на резисторах делителя определяется по формулам
UR1 = I*R1; UR2 = I*R2 (1)
где UR1, UR2 — падения напряжения на резисторах R1 и R2 соответственно, I — ток в цепи. В схемах делителей выходное напряжение обычно снимают с нижнего по схеме резистора.
Сумма падений напряжений UR1, UR2 на резисторах равна напряжению источника питания. Ток в цепи будет равен напряжению источника питания, делённому на сумму сопротивлений резисторов R1 и R2:
I = Uпит / (R1 + R2) (2)
Рассмотрим практическую схему делителя постоянного напряжения (рис.2)
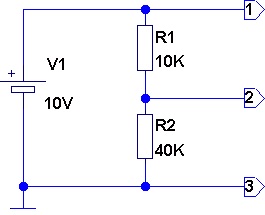
Рис. 2. Делитель постоянного напряжения.
Ток, протекающий в этой схеме, согласно формуле (2) будет равен
I = 10 / (10000+40000) = 0,0002 А = 0,2 мА.
Тогда согласно формуле (1) падение напряжения на резисторах делителя напряжения будет равно:
UR1 = 0,0002*10000 = 2 В;
UR2 = 0,0002*40000 = 8 В.
Если из формулы (1) вывести ток:
I = UR1 / R1 (3)
И подставить его значение в формулу (2), то получится универсальная формула для расчёта делителя напряжения:
UR1 / R1 = Uпит / (R1 + R2)
Откуда
UR1 = Uпит * R1 / (R1 + R2) (4)
Подставляя значения напряжения и сопротивлений в формулу (4), получим величину напряжения на резисторе R1:
UR1 = 10 * 10000 / (10000+40000) = 2 В,
и на резисторе R2:
UR2 = 10 * 40000 / (10000+40000) = 8 В.
Делитель напряжения с реактивными элементами в цепи переменного тока
В вышеприведённой схеме делителя напряжения (рис. 2) были использованы активные элементы — резисторы, и питание схемы осуществлялось постоянным напряжением (хотя схему можно питать и переменным током). Делитель напряжения может содержать так же и реактивные компоненты (конденсаторы, катушки индуктивности), но в этом случае для нормальной работы потребуется питание синусоидальным током (рис. 3).
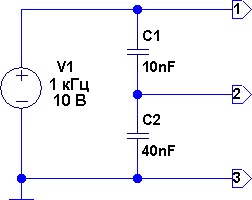
Рис. 3. Ёмкостный делитель напряжения в цепи переменного тока.
Изображённый на рисунке 3 ёмкостный делитель напряжения работает аналогично резистивному делителю, но рассчитывается несколько иначе, поскольку реактивное сопротивление конденсаторов обратно пропорционально их ёмкости:
Rc = 1/(2 * π * f * C)
Здесь Rc — реактивное сопротивление конденсатора;
π — число Пи = 3,14159…;
f — частота синусоидального напряжения, Гц;
C — ёмкость конденсатора, Фарад.
То есть чем больше ёмкость конденсатора, тем меньше его сопротивление, и следовательно в схеме делителя напряжения на конденсаторе с большей ёмкостью падение напряжения будет меньше, чем на конденсаторе с меньшей ёмкостью. Следовательно, формула (4) для ёмкостного делителя напряжения примет следующий вид:
UС1 = Uпит * С2 / (С1 + С2) (5)
UС1 = 10 * 40*10-9 / (10*10-9+40*10-9) = 8 В,
UС2 = 10 * 10*10-9 / (10*10-9+40*10-9) = 2 В.
Индуктивный делитель напряжения (рис. 4.) так же как и ёмкостный требует для своей работы синусоидальное питающее напряжение.
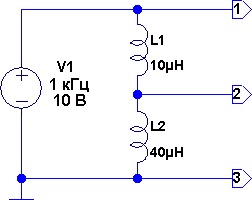
Рис. 4. Индуктивный делитель напряжения в цепи переменного тока.
Поскольку реактивное сопротивление катушки индуктивности в цепи переменного тока пропорционально номиналу катушки:
RL = 2 * π * f * L
Здесь Rc — реактивное сопротивление катушки индуктивности;
π — число Пи = 3,14159…;
f — частота синусоидального напряжения, Гц;
L — индуктивность катушки, Генри.
То следовательно и формула для расчёта индуктивного делителя напряжения будет точно такой же, как и формула для расчёта резистивного делителя напряжения (4), где вместо сопротивлений будут использоваться индуктивности:
UL1 = Uпит * L1 / (L1 + L2) (6)
Подставив в эту формулу параметры элементов из рисунка 4, получим:
UL1 = 10 * 10*10-6 / (10*10-6+40*10-6) = 2 В,
UL2 = 10 * 40*10-6 / (10*10-6+40*10-6) = 8 В.
В заключении следует отметить, что во всех расчётах величина нагрузки была принята равной бесконечности, поэтому полученные значения верны при работе рассмотренных делителей на сопротивление нагрузки, во много раз большее, чем величина собственных сопротивлений.