Даже самый последний лодырь, проучившись некоторое время в 10-м классе, скажет учителю, что закон Ома – это «U равно I, умноженному на R». К сожалению, самый умный отличник скажет ненамного больше – физическая сторона закона Ома останется для него тайной за семью печатями. Позволю себе поделиться с коллегами своим опытом изложения этой, на первый взгляд, примитивной темы.

Объектом моей педагогической деятельности был художественно-гуманитарный 10-й класс, чьи главные интересы, как догадывается читатель, лежали весьма далеко от физики. Именно поэтому преподавание этого предмета было возложено на автора этих строк, который, вообще говоря, преподаёт биологию. Было это несколько лет назад.

Урок про закон Ома начинается с тривиального утверждения, что электрический ток – это движение заряженных частиц в электрическом поле. Если на заряженную частицу действует только электрическая сила, то частица в соответствии со вторым законом Ньютона будет двигаться ускоренно. А если вектор электрической силы, действующей на заряженную частицу, будет на всей траектории постоянным, – то равноускоренно. Точно так же, как под действием силы тяжести падает гирька.

Но вот парашютист опускается совершенно не так. Если пренебречь ветром, то скорость его падения постоянна. Даже ученик художественно-гуманитарного класса ответит, что на падающий парашют помимо силы земного тяготения действует ещё одна сила – сила сопротивления воздуха. Эта сила равна по абсолютной величине силе притяжения парашюта Землёй и противоположна ей по направлению. Почему? Это ключевой вопрос урока. После некоторого обсуждения приходим к выводу, что сила сопротивления воздуха растёт с увеличением скорости падения. Поэтому падающее тело разгоняется до такой скорости, при которой сила тяжести и сила сопротивления воздуха уравниваются, и тело дальше падает с постоянной скоростью.

Правда, в случае парашютиста дело обстоит несколько сложнее. Парашют раскрывается не сразу, и парашютист разгоняется до значительно более высокой скорости. А когда парашют уже раскрылся, начинается падение с замедлением, которое продолжается до тех пор, пока сила тяжести и сила сопротивления воздуха не уравновешиваются.

Для груза на парашюте общей массой m, опускающегося с постоянной скоростью v , мы можем написать: mg – F( v ) = 0, где F( v ) – сила сопротивления воздуха, рассматриваемая как функция от скорости падения. По поводу вида функции F( v ) мы пока можем сказать лишь одно: она монотонно возрастает. Именно это обстоятельство обеспечивает стабилизацию скорости.

В наиболее простом случае, когда F( v ) = k, постоянная скорость, с которой будет падать парашют, окажется равной mg/k. Сделаем теперь некоторое преобразование. Пусть парашют падает с высоты h. Тогда разница потенциальных энергий тела до и после падения будет равна mgh = mU, где U – потенциальная энергия тела единичной массы на высоте h, или разность потенциалов гравитационного поля в начальной и конечной точках падения.

С учётом вышеизложенного получаем формулу: F( v ) = mU/h. (1)

А теперь вернёмся к проводнику, по которому течёт электрический ток. По проводнику движется большое количество заряженных частиц, которые сталкиваются с атомами тем чаще, чем быстрее летят. Аналогия со спуском парашюта достаточно прозрачна, разница лишь в том, что «парашютов» много и двигаются они не в гравитационном, а в электрическом поле. Учитывая эти обстоятельства, (1) можно переписать в виде: F( v ) = еU/l, (2)

где е – заряд частицы, U – разность электрических потенциалов на концах проводника, l – длина проводника. Сила тока, очевидно, равна I = neS, где n – число заряженных частиц в единице объёма, S – площадь поперечного сечения проводника, – скорость частицы (для простоты предположим, что все заряженные частицы одинаковы).

Чтобы получить зависимость I(U), нужно знать в явном виде зависимость F(). Наиболее простой вариант (F = k) сразу даёт закон Ома (I ~ U):

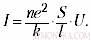
Величину называют проводимостью, а обратную ей величину – сопротивлением. В честь первооткрывателя закона сопротивление принято выражать в омах.

Величину (ne2/k) называют удельной проводимостью, а обратную ей величину – удельным сопротивлением. Эти величины характеризуют материал, из которого состоит проводник. Существенно, что удельная проводимость пропорциональна числу заряженных частиц в единице объёма (n). В металлах и растворах электролитов это число велико, а вот в диэлектриках мал. Число заряженных частиц в единице объёма газа может зависеть от приложенного поля (т.е. является функцией U), поэтому к газам закон Ома неприменим.

При выводе закона Ома мы сделали одно неочевидное предположение. Мы приняли, что сила, тормозящая движение заряженной частицы, пропорциональна скорости её движения. Конечно, можно было бы попытаться как-то обосновать эту идею, но экспериментальная проверка выглядит куда убедительнее.

Экспериментальной проверкой этого предположения явится, очевидно, проверка самого закона Ома, т.е. пропорциональности U и I. Казалось бы, это сделать несложно: у нас есть вольтметр и амперметр! Увы, всё не так просто. Приходится объяснять ученикам, что вольтметр, так же, как и амперметр, измеряет не напряжение, а силу тока. И ставить на шкале вольтметра вольты мы имеем право лишь потому, что изначально знаем закон Ома, который и хотим проверить. Нужны другие подходы.

Можно, например, использовать следующую идею. Соединим последовательно n батарей и предположим, что напряжение при этом увеличилось в n раз. Если закон Ома верен, то сила тока тоже увеличится в n раз, из-за чего отношение n/I(n) от величины n зависеть не будет. Это предположение оправдывается на опыте. Правда, батареи тоже имеют внутреннее сопротивление, из-за чего величина n/I(n) медленно растёт при увеличении n, однако поправку на это сделать нетрудно. (Сам Г. Ом измерял напряжение по-другому, о чём ученики могут прочитать в учебнике Г.Я.Мякишева и др.)

Задаём вопрос: «“В далёком созвездии Тау Кита” действует не закон Ома, а закон великого местного учёного академика Икс. Согласно закону Икса, сила тока пропорциональна квадрату разности потенциалов на концах проводника. Как на Тау Кита зависит сила торможения частиц от их скорости?» С помощью несложных преобразований ученики приходят к выводу, что сила пропорциональна корню квадратному из скорости.

А теперь перейдём к другому процессу: движению воды в трубе, на концах которой созданы разные давления. Здесь перед нами совершенно другая ситуация: не отдельные движущиеся частицы трутся о неподвижный материал, распределённый по всему объёму проводника, а слои движущихся частиц трутся друг о друга. И это обстоятельство коренным образом изменяет все физические рассуждения.

На отдельный слой движущейся в трубе воды действуют две силы:

а) разность сил давления на торцах слоя;

б) сила трения о соседние слои воды.

Если установилась постоянная скорость движения слоя, то эти силы равны и направлены в противоположные стороны.

Сила трения о соседние слои воды может тормозить движение в том и только в том случае, если разные слои воды движутся с разными скоростями. В проводнике скорость заряженных частиц не зависит от того, находятся ли они у края проводника или в его центре, а вот вода в центре трубы движется быстро, а по краям – медленно, на самой же поверхности трубы скорость воды равна нулю.

Аналогом силы тока можно считать расход воды, т.е. количество воды, вытекающее из трубы в единицу времени. Поскольку скорость воды в разных слоях неодинакова, рассчитать расход не так просто. Аналог разности электрических потенциалов – разность давлений на концах трубы.

Так же, как и в проводнике с током, в трубе с водой наблюдается прямая пропорциональность между разностью давлений на концах и расходом. А вот коэффициент пропорциональности совершенно иной. Во-первых, расход воды зависит не только от площади поперечного сечения трубы, но и от его формы. Если труба цилиндрическая, то расход прямо пропорционален не площади поперечного сечения, а её квадрату (т.е. радиусу в четвёртой степени). Эта зависимость носит название закона Пуазейля.

Тут самое время вспомнить курс анатомии, физиологии и гигиены, изучавшийся в 9-м классе. В организме человека имеется большое количество параллельно соединённых сосудов. Предположим, что один из этих сосудов расширился, и его радиус немного, всего в два раза, увеличился. Во сколько раз, при том же давлении на концах сосуда, возрастёт количество проходящей через него крови? Площадь поперечного сечения пропорциональна квадрату радиуса, а квадрат площади поперечного сечения – радиусу в четвёртой степени. Следовательно, при увеличении радиуса в два раза поток крови увеличивается в 16 (!) раз. Такова сила закона Пуазейля, позволяющего создать очень эффективный механизм перераспределения крови между органами. Если бы по кровеносным сосудам текла не кровь, а электроны, то их поток вырос бы всего в четыре раза.

Описанное выше изложение темы отличается от традиционного. Во-первых, на тему тратится три урока, что при нынешнем дефиците часов на естественные науки может рассматриваться как непозволительная роскошь. Однако это оправдывается тем, что удаётся достаточно просто и популярно вскрыть физический смысл закона и вооружить учащихся методологией, которую они могут использовать при анализе самых разных физических процессов: падения тела в воздухе, движения жидкости в трубе, движения заряженных частиц по проводнику, а позже – при анализе прохождения электрического тока через вакуум и через газы.

Этот подход называется внутрипредметной интеграцией. С его помощью мы продемонстрировали учащимся общие черты в далёких, на первый взгляд, друг от друга разделах физики, показали, что физика – это не «куча» не связанных друг с другом «физических законов», а стройное здание. То же самое справедливо, разумеется, и для других научных дисциплин. И поэтому, казалось бы, нерациональная трата учебных часов вполне окупается.

В заключение считаю своим долгом выразить глубразить глубокую благодарность моим бывшим коллегам – преподавателям физики Г.П.Дегтярёвой и Г.В.Кобцевой за полезные советы и плодотворные дискуссии.

С.В.БАГОЦКИЙ < b1949@mail.ru>, к.б.н., МИОО, г. Москва

Читайте также: Как пользоваться мультиметром