В 1202 г. итальянский математик Леонардо Фибоначчи опубликовал свою работу под названием «Книга абака» («Книга расчетов»), в которой описал также увековечившие его имя числовые ряды. В одной из глав Фибоначчи пытается математически показать, каким образом будет увеличиваться количество кроликов. Он рассматривал следующие гипотезы в качестве условий:
1) первые два месяца пара кроликов не дает потомства;
2) начиная с третьего месяца пара кроликов дает еще одну пару кроликов.

В результате построения схемы роста популяции кроликов, получаем следующий ряд чисел, отмечающий увеличение количества кроликов каждый месяц:
1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144 …
1 + 1 = 2; 1 + 2 = 3; 2 + 3 = 5; 3 + 5 = 8…
Если вы внимательно посмотрите на шишку, вы увидите, что ее поверхность состоит из чешуек, которые закручиваются по спирали в соответствии с последовательностью Фибоначчи. В то время как в ананасе или в цветке подсолнуха они видны невооруженным глазом.

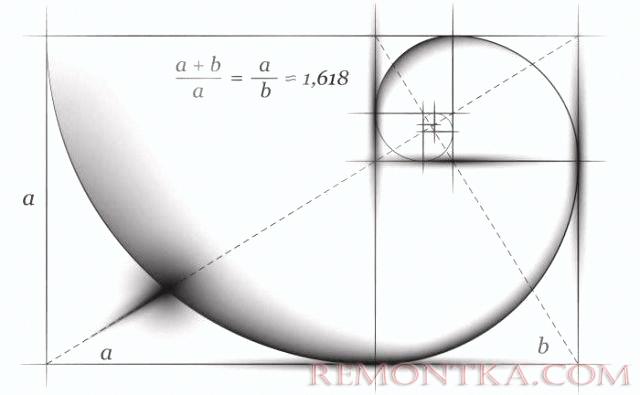
Со времен Античности золотого сечение — число = 1,618. Древние Греки считали значением идеальной пропорции. Золотое сечение — это отношение каждого последующего числа в ряде Фибоначчи к предыдущему:
144/89=89/55=55/34=34/21=21/13=13/8=8/5=5/3=1,618…
Древние Греки использовали его в архитектуре. Фасад Парфенона в Афинах имеет очень схожие пропорции с прямоугольником, построенным по принципу золотого сечения.
Так в чем же красота последовательности сечений проводов, номинальных токов электрических и токов отсечки автоматических выключателей? Построим ряд чисел со следующими значениями: 1,5; 2,5; 4; 6; 10; 16; 25 ; 40 ; 63…

Номинальные токи электромагнитных пускателей:

Так вот если разделить 2,5/1,5; 4/2,5; 6,3/4; 10/6,3; 16/10; 25/16 ; 40/25 ; 63/40 , то мы получим приблизительно 1,6. Что соответствует правилу золотого сечения. И отражает красоту и гениальность природы даже в наших нудных инженерных системах.
А вы как думаете? Это случайность?
По мотивам книги «Большой роман о математике. История мира через призму математики» Микаэля Лонэ. Спасибо за рекомендацию от Владимир Кисель.
Информация, опубликованная на данном веб-сайте, представлена исключительно в ознакомительных целях, за применение этой информации администрация сайта ответственности не несет.